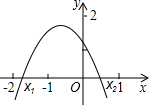Question

将二次函数y=2x²+4x-6的图象在x轴下方的部分沿x轴翻折，得到一个新图象，当直线y=

1

2

x+b与此图象有两个公共点时，则b的取值范围为______．

Answer 1

二次函数y=2x²+4x-6的图象在x轴下方的部分沿x轴翻折，
∴令2x²+4x-6=0，
解之得：x₁=1，x₂=-3，
故图象与x轴的交点坐标分别为（1，0），B（-3，0），
如图，当直线y=

1

2

x+b经过点（1，0）时，可得b=-

1

2

，
当直线y=

1

2

x+b经过点（-3，0）时，
可得b=

3

2

．
由图可知符合题意的b的取值范围为：-

1

2

＜b＜

3

2

．
故答案为：-

1

2

＜b＜

3

2

．