题目内容
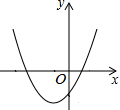
二次函数y=ax2+bx+c的图象如图所示，则abc，b2-4ac，2a+b，a+b+c这四个式子中，请分别判断其值的符号并说明理由．答：______．
（1）abc＞0，理由是，
抛物线开口向上，a＞0，
抛物线交y轴负半轴，c＜0，
又对称轴交x轴的正半轴，-
＞0，而a＞0，得b＜0，
因此abc＞0；
（2）b2-4ac＞0，理由是，
抛物线与x轴有两个交点，b2-4ac＞0；
（3）2a+b＞0，理由是，
-
＜1，a＞0，∴-b＜2a，因此2a+b＞0；
（4）a+b+c＜0，理由是，
由图象可知，当x=1时，y＜0；而当x=1时，y=a+b+c．即a+b+c＜0．
抛物线开口向上，a＞0，
抛物线交y轴负半轴，c＜0，
又对称轴交x轴的正半轴，-
| b |
| 2a |
因此abc＞0；
（2）b2-4ac＞0，理由是，
抛物线与x轴有两个交点，b2-4ac＞0；
（3）2a+b＞0，理由是，
-
| b |
| 2a |
（4）a+b+c＜0，理由是，
由图象可知，当x=1时，y＜0；而当x=1时，y=a+b+c．即a+b+c＜0．
练习册系列答案
阅读快车系列答案
相关题目
