题目内容

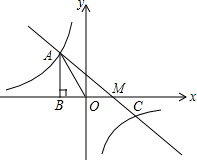
如图，A、B是反比例函数y=
k
x
（k＞0）上得两个点，AC⊥x轴于点C，BD⊥y轴于点D，连接AD、BC，则△ABD与△ACB的面积大小关系是（　　）
A．S△ADB＞S△ACBB．S△ADB＜S△ACB
C．S△ADB=S△ACBD．不确定

设A的横坐标是a，则纵坐标是
k
a
，
当B的横坐标是b时，则纵坐标是：
k
b
．
则△ABD的面积是：
1
2
b•（
k
a
-
k
b
）=
b2k-abk
2ab
=
(b-a)k
2a
；
△ACB的面积是：
1
2
•
k
a
（b-a）=
(b-a)k
2a
．
故△ABD的面积=△ACB的面积．
故选C．
练习册系列答案
相关题目
已知反比例函数y=
k
x
图象过第二象限内的点A（-2，m），作AB⊥x轴于点B，Rt△AOB面积为3．
（1）求k和m的值；
（2）若直线y=ax+b经过点A，并且经过反比例函数y=
k
x
的图象上另一点C（4，-
3
2
）
①求直线y=ax+b关系式；
②设直线y=ax+b与x轴交于M，求AM的长；
③根据图象写出使反比例函数y=
k
x
值大于一次函数y=ax+b的值的x的取值范围．
已知，如图：点A（
3
，1）在反比例函数图象上，将y轴绕点O顺时针旋转30°，与反比例函数在第一象限内交于点B，
求：（1）反比例函数的解析式；
（2）求点B的坐标及△AOB的面积．
根据图（1）所示的程序，得到了y与x的函数，其图象如图（2）所示．若点M是y轴正半轴上任意一点，过点M作PQ∥x轴交图象于点P，Q，连接OP，OQ．以下结论：
①x＜0时，y=-
2
x
；
②x＜0时，y随x的增大而减小；
③PQ=3PM；
④∠POQ可以等于90°；
则其中正确结论有（　　）
A．1个B．2个C．3个D．4个
两个反比例函数y=
3
x
，y=
6
x
在第一象限内的图象如图所示，点P1，P2，P3，…，P2011：在反比例函数y=
6
x
图象上，它们的横坐标分别是x1，x2，x3，…，x2011，纵坐标分别是1，3，5，…，共2011个连续奇数，过点P1，P2，P3，…，P2011分别作y轴的平行线，与y=
3
x
的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2011（x2011，y2011），则y2011=______．
如图，Rt△OAB的斜边OA在x轴上，点B在第一象限，OA：OB=5：4．边AB的垂直平分线分别交AB、x轴于点C、D，线段CD交反比例函数y=
3
x
的图象于点E．当BC=CE时，以DE为边的正方形的面积是（　　）
A．
25
29
B．1C．
30
29
D．
36
29
如图（1），正方形ABCD和正方形AEFG的边AB和AG在同一条直线上．

（1）判断C、A、F是否在同一条直线上，说明理由？
（2）如图（2）以直线AB为x轴，线段AG的垂直平分线为y轴建立平面直角坐标系，已知OA=AB=1，判断点C、点F是否在同一个反比例函数的图象上？若在，求出这个函数的解析式；若不在，说明理由．
（3）若将（2）中的条件改为0A=AB=m，请完成（2）中的问题．
如图，反比例函数y=
k
x
（k＞0）与长方形OABC在第一象限相交于D、E两点，OA=2，OC=4，连接OD、OE、DE．记△OAD、△OCE的面积分别为S1、S2．
（1）①点B坐标为______；②S1______S2（填“＞”、“＜”、“=”）；
（2）当点D为线段AB的中点时，求k的值及点E坐标；
（3）当S1+S2=2时，试判断△ODE的形状，并求△ODE的面积．
李先生参加了清华同方电脑公司推出的分期付款购买电脑活动，他购买的电脑价格为1.2万元，交了首付之后每月付款y元，x月结清余款．y与x的函数关系如图所示，试根据图象提供的信息回答下列问题．
（1）确定y与x的函数关系式，并求出首付款的数目；
（2）如打算每月付款不超过500元，李先生至少几个月才能结清余款？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网