Question

如图（1），正方形ABCD和正方形AEFG的边AB和AG在同一条直线上．

（1）判断C、A、F是否在同一条直线上，说明理由？
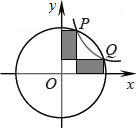
（2）如图（2）以直线AB为x轴，线段AG的垂直平分线为y轴建立平面直角坐标系，已知OA=AB=1，判断点C、点F是否在同一个反比例函数的图象上？若在，求出这个函数的解析式；若不在，说明理由．
（3）若将（2）中的条件改为0A=AB=m，请完成（2）中的问题．

Answer 1

（1）∵AB和AG在同一条直线上，
∴∠EAB=90°，
∵AF、AC分别是正方形的对角线，
∴∠EAF=∠BAC=45°，
∴∠FAC=∠FAE+∠EAB+∠BAC=180°，
故C、A、F在同一条直线上．

（2）由题意得，OA=AB=1，
结合直角坐标系可得点C的坐标为（2，-1），点F的坐标为（-1，2），
设过点C的反比例函数关系式为y=

k

x

，将点C代入可得：-1=

k

2

，
解得：k=-2，即反比例函数关系式为y=-

2

x

，
将点F（-1，2）代入可得：2=-

2

-1

，从而可得点F也在经过点C的反比例函数上．
即点C、点F是否在同一个反比例函数的图象上，这个反比例函数为y=-

2

x

．

（3）由题意得，OA=AB=m，
结合直角坐标系可得点C的坐标为（2m，-m），点F的坐标为（-m，2m），
设过点C的反比例函数关系式为y=

k

x

，将点C代入可得：-m=

k

2m

，
解得：k=-2m²，即反比例函数关系式为y=-

2m2

x

，
将点F（-m，2m）代入可得：2m=-

2m2

-m

，从而可得点F也在经过点C的反比例函数上．
即点C、点F是否在同一个反比例函数的图象上，这个反比例函数为y=-

2m2

x

．