题目内容
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
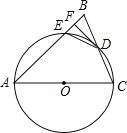
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
【答案】(1)见解析;(2)9
【解析】
试题分析:(1)连接OD,利用AB=AC,OD=OC,证得OD∥AD,易证DF⊥OD,故DF为⊙O的切线;
(2)证得△BED∽△BCA,求得BE,利用AC=AB=AE+BE求得答案即可.
(1)证明:如图,

连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴![]() =
=![]() ,
,
∵OD∥AB,AO=CO,
∴BD=CD=![]() BC=3,
BC=3,
又∵AE=7,
∴![]() =
=![]() ,
,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目