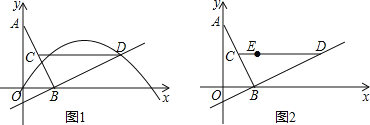题目内容
【题目】如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数![]() 的图象的两个交点.
的图象的两个交点.

(1)填空:点E坐标: ;不等式![]() 的解集为 ;
的解集为 ;
(2)求正比例函数和反比例函数的关系式;
(3)P(m,n)是函数![]() 图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
【答案】(1)(﹣3,﹣2),x>3或﹣3<x<0;(2)y=![]() x,y=
x,y=![]() (3)
(3)![]()
【解析】
试题分析:(1)点E的坐标是点A关于坐标原点的中心对称点,所以点E(﹣3,﹣2),观察图象即可求得不等式![]() 的解集.
的解集.
(2)把A的坐标代入解析式求出a、k即可;
(3)P为线段BD的中点求出P点的坐标值,然后用矩形的面积减去三个三角形的面积即可.
解:(1)点E坐标:(﹣3,﹣2),
不等式![]() 的解集为:x>3或﹣3<x<0.
的解集为:x>3或﹣3<x<0.
(2)把A(3,2)代入y=ax
得:2=3a,
解得:a=![]() ,
,
∴y=![]() x,
x,
代入y=![]()
得:k=6,
∴y=![]() ,
,
∴正比例函数与反比例函数的解析式分别是y=![]() x,y=
x,y=![]() .
.
(3)∵P为线段BD的中点,BD=OC=3,
∴P点的横坐标为![]() ,
,
代入y=![]() ,
,
得y=4,
∴P(![]() ,4);
,4);
S△AOP=S矩形OCDB﹣S△AOC﹣S△BOP﹣S△APD=3×4﹣![]() ×2×3﹣
×2×3﹣![]() ﹣
﹣![]() =
=![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目