题目内容
如图,已知反比例函数y=| k |
| x |
| m-3 |
| m-2 |
| 3 |
| 2-m |
(1)试判断四边形PAOB的形状,并说明理由;
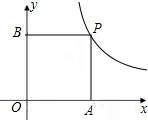
(2)连接AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连接OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明;
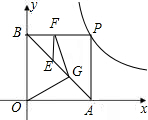
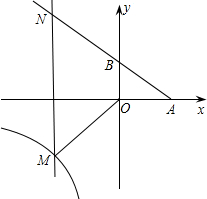
(3)若M为反比例函数y=
| k |
| x |
分析:(1)解出分式方程得到m的值,进而可判断出四边形PAOB的形状;
(2)应猜想相等,找这两条线段所在三角形全等的条件;
(3)易知∠BNM=45°,要想为等腰梯形,∠OMN=45°,那么点M的横纵坐标相等.代入反比例函数即可.
(2)应猜想相等,找这两条线段所在三角形全等的条件;
(3)易知∠BNM=45°,要想为等腰梯形,∠OMN=45°,那么点M的横纵坐标相等.代入反比例函数即可.
解答:解:(1)四边形PAOB是正方形.
理由如下:
∵∠AOB=∠OBP=∠OAP=90°
∴四边形PAOB是矩形(2分)
m-3+m-2=-3
解得:m=1
经检验知m=1是原分式方程的解
∴P(2,2)(3分)
∴PB=PA=2
∴四边形PAOB是正方形;(4分)
(2)OG=FG.
证明:延长FE交OA于点H,连接GH,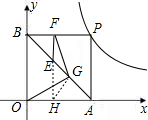
∵∠HFB=∠FBO=∠BOH=90°
∴BOHF是矩形
∴BF=OH
∵∠FBE=∠FEB=45°
∴EF=BF=OH(5分)
∵∠EHA=90°,G为AE的中点
∴GH=GE=GA(6分)
∴∠GEH=∠GAH=45°
∴∠GEF=∠GHO(7分)
∴△GEF≌△GHO
∴OG=FG;(8分)
(3)由题意知:∠BNM=45°(9分)
∵要让四边形OBNM为等腰梯形
∴∠BNM=∠NMO=45°(10分)
∴设M点的坐标为(x,x),代入y=
∴x=±2
∵M是y=
第三象限上一动点
∴x=-2
∴M点的坐标为(-2,-2).(12分)
理由如下:
∵∠AOB=∠OBP=∠OAP=90°
∴四边形PAOB是矩形(2分)
m-3+m-2=-3
解得:m=1
经检验知m=1是原分式方程的解
∴P(2,2)(3分)
∴PB=PA=2
∴四边形PAOB是正方形;(4分)
(2)OG=FG.
证明:延长FE交OA于点H,连接GH,

∵∠HFB=∠FBO=∠BOH=90°
∴BOHF是矩形
∴BF=OH
∵∠FBE=∠FEB=45°
∴EF=BF=OH(5分)
∵∠EHA=90°,G为AE的中点
∴GH=GE=GA(6分)
∴∠GEH=∠GAH=45°
∴∠GEF=∠GHO(7分)
∴△GEF≌△GHO
∴OG=FG;(8分)
(3)由题意知:∠BNM=45°(9分)

∵要让四边形OBNM为等腰梯形
∴∠BNM=∠NMO=45°(10分)
∴设M点的坐标为(x,x),代入y=
| 4 |
| x |
∴x=±2
∵M是y=
| k |
| x |
∴x=-2
∴M点的坐标为(-2,-2).(12分)
点评:证线段相等,通常是证明线段所在的三角形全等;等腰梯形同一底上的两个角是相等的;函数图象过某个点,这个点的坐标应适合这个函数解析式.

练习册系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=