Question

【题目】如图，已知∠DAE=∠B，∠DAB=∠C，则下列结论不成立的是（ ）

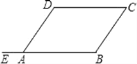
A.AD∥BCB.AB∥CDC.∠DAB+∠B=180°D.∠B=∠C

Answer 1

【答案】D

【解析】

由∠DAE=∠B依据“同位角相等，两直线平行”即可得出AD∥BC即A成立；依据“两直线平行，同旁内角互补”可得出∠DAB+∠B=180°，即C成立；由等量替换即可得出∠B+∠C=180°，即B成立；无法判断D是否成立．由此即可得出结论．

解：A．∵∠DAE=∠B，

∴AD∥BC，故A成立；

C．∵AD∥BC，

∴∠DAB+∠B=180°，

∵∠DAB=∠C，

∴∠B+∠C=180°，故C成立；

B．∵∠B+∠C=180°，

∴AB//CD，故B成立；

D．无法证明∠B=∠C，故D不成立；

故选：D．