题目内容
【题目】如图在![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 点沿线段
点沿线段![]() 向
向![]() 点运动,以
点运动,以![]() 为斜边在
为斜边在![]() 右侧作等腰直角三角形
右侧作等腰直角三角形![]() 则
则![]() 的最小值为_____________________.
的最小值为_____________________.
【答案】![]()
【解析】
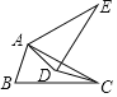
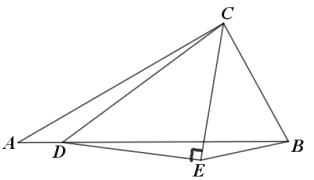
以AC为斜边,在AC右侧作等腰直角三角形AE1C,边E1C与AB交与点G,连接E1E延长与AB交于点F,连接CF,作BE2⊥E1F于点E2.因为Rt△DCE与Rt△AE1C为等腰直角三角形,可得∠DCE=∠CDE=∠ACE1=∠CAE1=45°,于是∠ACD=∠E1CE,所以∠CAD=∠CE1E=30°,所以E在直线E1E上运动,当BE2⊥E1F时,BE最短,即为BE2的长.
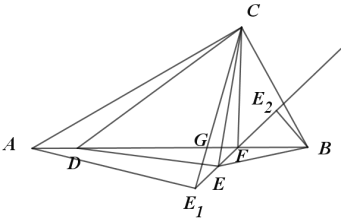
以AC为斜边,在AC右侧作等腰直角三角形AE1C,边E1C与AB交与点G,连接E1E延长与AB交于点F,连接CF,作BE2⊥E1F于点E2,因此△ACD∽△E1CE
∵Rt△DCE与Rt△AE1C为等腰直角三角形
∴∠DCE=∠CDE=∠ACE1=∠CAE1=45°
∴∠ACD=∠E1CE
∵![]()
∴△ACD∽△E1CE
∴∠CAD=∠CE1E=30°
∵D在AB上运动,
∴E在直线E1E上运动
当BE2⊥E1F时,BE最短,即为BE2的长
在△AGC与△E1GF中
∠AGC=∠E1GF,∠CAG=GE1F
∴∠GFE1=∠ACG=45°
∴∠CAD=∠CE1F=30°
∴点A,C,F,E1四点共圆
∴∠AE1C=∠ACF=90°,且∠ABC=60°,则∠BCF=30°
∵AC=6
∴BC=![]()
∴BF=![]()
∴BE2=![]()
故答案是![]()

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目