题目内容
已知反比例函数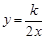 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.
(1)求反比例函数的解析式;
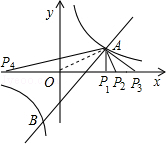
(2)求反比例函数与一次函数两个交点A、B的坐标:
(3)根据函数图像,求不等式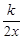 >2x-1的解集;
>2x-1的解集;
(4)在(2)的条件下, x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.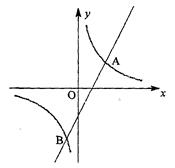
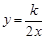 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.(1)求反比例函数的解析式;
(2)求反比例函数与一次函数两个交点A、B的坐标:
(3)根据函数图像,求不等式
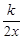 >2x-1的解集;
>2x-1的解集;(4)在(2)的条件下, x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.

(1)∵一次函数的图象经过(a,b),(a+k,b+k+2)两点,
∴b=2a﹣1①,2a+2k﹣1=b+k+2②,
∴整理②得:b=2a﹣1+k﹣2,
∴由①②得:2a﹣1=2a﹣1+k﹣2,
∴k﹣2=0,
∴k=2,
∴反比例函数的解析式为:y=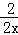 =
= ;
;
(2)解方程组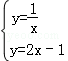 ,
,
解得: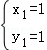 ,
,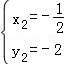 ,
,
∴A(1,1),B(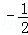 ,﹣2);
,﹣2);
(3)根据函数图象,可得出不等式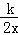 >2x﹣1的解集;
>2x﹣1的解集;
即0<x<1或x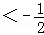 ;
;
(4)当AP1⊥x轴,AP1=OP1,∴P1(1,0),
当AO=OP2,∴P2(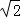 ,0),
,0),
当AO=AP3,∴P3(2,0),
当AO=P4O,∴P4(﹣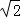 ,0).
,0).
∴存在P点P1(1,0),P2(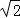 ,0),P3(2,0),P4(﹣
,0),P3(2,0),P4(﹣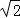 ,0).
,0).
∴b=2a﹣1①,2a+2k﹣1=b+k+2②,
∴整理②得:b=2a﹣1+k﹣2,
∴由①②得:2a﹣1=2a﹣1+k﹣2,
∴k﹣2=0,
∴k=2,
∴反比例函数的解析式为:y=
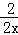 =
= ;
;(2)解方程组
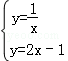 ,
,解得:
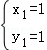 ,
,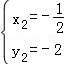 ,
,∴A(1,1),B(
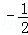 ,﹣2);
,﹣2);(3)根据函数图象,可得出不等式
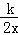 >2x﹣1的解集;
>2x﹣1的解集;即0<x<1或x
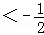 ;
;(4)当AP1⊥x轴,AP1=OP1,∴P1(1,0),
当AO=OP2,∴P2(
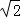 ,0),
,0),当AO=AP3,∴P3(2,0),
当AO=P4O,∴P4(﹣
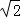 ,0).
,0).∴存在P点P1(1,0),P2(
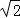 ,0),P3(2,0),P4(﹣
,0),P3(2,0),P4(﹣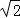 ,0).
,0).
(1)将点(a,b),(a+k,b+k+2)分别代入一次函数解析式,即可得出关于b的等式,即可得出答案;
(2)利用(1)中k的值,得出反比例函数解析式,将两函数组成方程组,求出交点坐标即可;
(3)利用函数图象交点坐标,即可得出不等式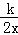 >2x﹣1的解集;
>2x﹣1的解集;
(4)分别根据当AP1⊥x轴时,当AO=OP2时,当AO=AP3时,当AO=P4O时,得出答案即可.
(2)利用(1)中k的值,得出反比例函数解析式,将两函数组成方程组,求出交点坐标即可;
(3)利用函数图象交点坐标,即可得出不等式
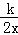 >2x﹣1的解集;
>2x﹣1的解集;(4)分别根据当AP1⊥x轴时,当AO=OP2时,当AO=AP3时,当AO=P4O时,得出答案即可.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 的图像在第二象限交于点B(4,n),(1)求n的值 (2)求一次函数的解析式.
的图像在第二象限交于点B(4,n),(1)求n的值 (2)求一次函数的解析式.
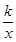 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为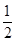 .
.
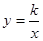 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线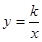 (x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.
(x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.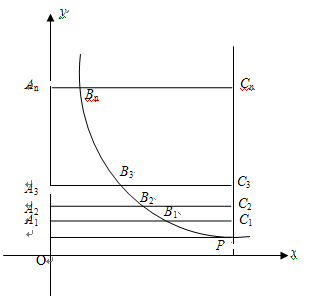
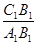 及
及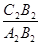 的值;
的值;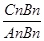 的值(直接写答案).
的值(直接写答案).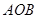 的顶点
的顶点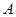 在反比例函数
在反比例函数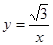 (
(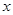 >0)的图象上,则点
>0)的图象上,则点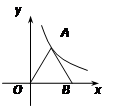
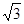 )
)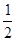 ,
,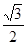 )
)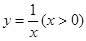 与直角边AB交于点C,与斜边OB交于点D,
与直角边AB交于点C,与斜边OB交于点D,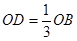 ,则△OBC的面积为 .
,则△OBC的面积为 .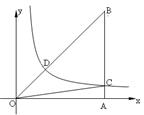
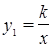 (x<0)上,AB⊥x轴,△AOB的面积为2,当直线
(x<0)上,AB⊥x轴,△AOB的面积为2,当直线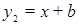 与
与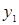 只有一个交点时,b= ▲ .
只有一个交点时,b= ▲ .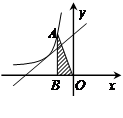
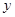 cm与宽
cm与宽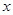 cm之间的函数关系用图象表示大致是
cm之间的函数关系用图象表示大致是 