题目内容
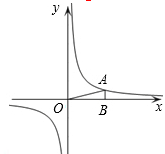
如图,在直角坐标系中,O为坐标原点. 已知反比例函数y=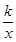 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为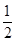 .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=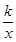 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y=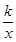 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
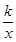 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为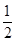 .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=
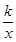 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;(3)过原点O的直线l与反比例函数y=
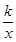 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值. (1)m=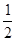 k=1(2)
k=1(2)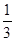 ≤y≤1(3)2
≤y≤1(3)2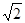
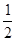 k=1(2)
k=1(2)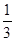 ≤y≤1(3)2
≤y≤1(3)2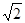
解:(1)∵A(2,m) ∴OB=2 AB=m
∴S△AOB=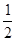 •OB•AB=
•OB•AB=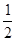 ×2×m=
×2×m=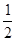 ∴m=
∴m=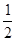 ……………………2分
……………………2分
∴点A的坐标为(2,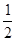 ) 把A(2,
) 把A(2,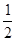 )代入y=
)代入y= ,得
,得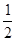 =
=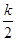
∴k="1" ………………………………………………………………………4分
(2)∵当x=1时,y=1;当x=3时,y=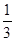 ……………………………………6分
……………………………………6分
又 ∵反比例函数y=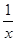 在x>0时,y随x的增大而减小……………………7分
在x>0时,y随x的增大而减小……………………7分
∴当1≤x≤3时,y的取值范围为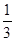 ≤y≤1 ……………………………8分
≤y≤1 ……………………………8分
(3) 由图象可得,线段PQ长度的最小值为2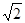 ……………………10分
……………………10分
(1)通过三角形的面积可求得m的值,即可求出点A的坐标,从而求得k的值
(2)把x的值分别代入求得y的值,再根据函数的增减性求得y的取值范围
(3)根据勾股定理求得线段PO的长,从而求得线段PQ长度的最小值
∴S△AOB=
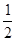 •OB•AB=
•OB•AB=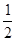 ×2×m=
×2×m=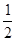 ∴m=
∴m=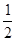 ……………………2分
……………………2分∴点A的坐标为(2,
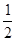 ) 把A(2,
) 把A(2,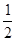 )代入y=
)代入y= ,得
,得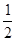 =
=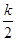
∴k="1" ………………………………………………………………………4分
(2)∵当x=1时,y=1;当x=3时,y=
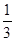 ……………………………………6分
……………………………………6分又 ∵反比例函数y=
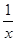 在x>0时,y随x的增大而减小……………………7分
在x>0时,y随x的增大而减小……………………7分∴当1≤x≤3时,y的取值范围为
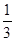 ≤y≤1 ……………………………8分
≤y≤1 ……………………………8分(3) 由图象可得,线段PQ长度的最小值为2
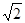 ……………………10分
……………………10分(1)通过三角形的面积可求得m的值,即可求出点A的坐标,从而求得k的值
(2)把x的值分别代入求得y的值,再根据函数的增减性求得y的取值范围
(3)根据勾股定理求得线段PO的长,从而求得线段PQ长度的最小值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

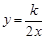 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.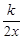 >2x-1的解集;
>2x-1的解集;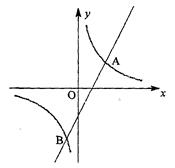
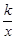 的图像经过点A(-
的图像经过点A(-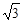 ,1)。
,1)。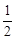 ,设Q点的纵坐标为n, 求n2-2
,设Q点的纵坐标为n, 求n2-2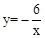 和
和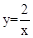 于A,B两点,P是x轴上的任意一点,则△ABP的面积等于 ▲ .
于A,B两点,P是x轴上的任意一点,则△ABP的面积等于 ▲ . 上的点,A,B两点的横坐标分别是a,2a,线段AB的延长线交x轴于点C,若
上的点,A,B两点的横坐标分别是a,2a,线段AB的延长线交x轴于点C,若 ,则k=___________.
,则k=___________.
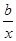 ,在同一坐标系中的大致图象可能是( )
,在同一坐标系中的大致图象可能是( )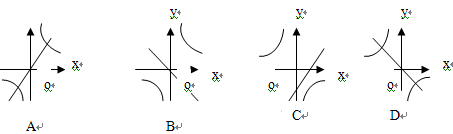
 ,AQ=
,AQ= ,求
,求
 面积是8,长为
面积是8,长为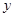 ,宽为
,宽为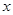 .则
.则