题目内容
如图,在Rt△ABC中,∠ACB=90°,A、B在x轴上,A(-1,0),C(0,-2),B在x轴正半轴上,求经过A、B、C三点的抛物线,并求此抛物线的顶点坐标.
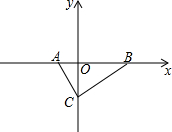

依题意,设B点坐标为(b,0)
则由直角三角形性质得,5+4+b2=(b+1)2,
结合图象解得,b=4,
即B(4,0).
设该抛物线为y=a(x+1)(x-4),
将点B代入解得,a=
将抛物线化为顶点式得y=
(x-
)2-
,
所以顶点为(
,-
).
则由直角三角形性质得,5+4+b2=(b+1)2,
结合图象解得,b=4,
即B(4,0).
设该抛物线为y=a(x+1)(x-4),
将点B代入解得,a=
| 1 |
| 2 |
将抛物线化为顶点式得y=
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
所以顶点为(
| 3 |
| 2 |
| 25 |
| 8 |

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目

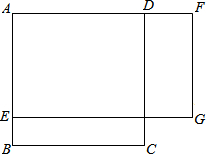
 绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).