题目内容

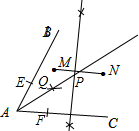
如图，1班的同学跟3班的同学分别在M、N两处参加植树活动，现在要在道路AB与道路AC的交叉区域设茶水供应点P，使它到两边的距离相等且PM=PN．
（1）画出点P（保留作图痕迹）
（2）说明理由．
（1）如图所示：A点为圆心，以任意长为半径画弧，交AB与AC于点E、F，
再分别以E、F为圆心，大于
1
2
EF长为半径画弧，交于点Q，连接AQ．
即AQ为∠BAC的角平分线．
连接MN，作MN的垂直平分线交AQ于P点．P点即为所求．

（2）理由如下：∵点P在∠BAC的平分线上，
∴点P到AC、AB的距离相等；
又∵点P在线段MN的垂直平分线上，
∴PM=PN．
练习册系列答案
相关题目
一个底面为正六边形的直六菱形的主视图和俯视图如图所示，则其左视图的面积为（　　）
A．8
3
B．8+8
3
C．16D．2+2
3
如图，已知：AB．
求作：（1）确定AB的圆心O；
（2）过点A且与⊙O相切的直线；
（注：作图要求利用直尺和圆规，不写作法，但要求保留作图痕迹）
如图，平面内有三个不在同一直线上的点A，B，C，按下列要求画图．（画图工具不限）
（1）画直线AB；
（2）画射线AC；
（3）连结B，C两点的线段；
（4）过点C作直线AB的平行线；
（5）过点C画直线AB的垂线PD，垂足为D；
（6）比较线段CA，CD，CB的长，并用“＜”号表示它们的长短关系．
如图，已知∠α、∠β．
（1）画∠AOB，使∠AOB=∠AOC+∠COB，且∠AOC=∠α，∠COB=∠β；
（2）在（1）所画的图中，画∠AOB的角平分线OD；
（3）在（1）（2）的前提下，如果∠AOB=110°，∠COD=30°，那么∠α、∠β的度数分别为多少度？
若一个长方形最少能分割成n个正方形，那么称n是这个正方形的“阶数”．如长为2，宽为1的长方形，可以分割为2个正方形，也可以分割为5个正方形，也可以分割为8个正方形：

因为这个长方形最少能分割为2个正方形，我们说它的“阶数”是2．
（1）长为6，宽为1的长方形，它的“阶数”是______；
（2）若长为a（a大于1），宽为1的长方形的“阶数”是3，请你画出图形，并求a的所有可能的值；
（3）现有一个长为11a，宽为8a（a大于0）的长方形，求它的“阶数”，并画图说明．
读下面的语句，并画图形．
（1）P是直线AB外的一点，直线CD经过点P，且与直线AB平行；直线EF经过点P，且与AB垂直，垂足为点G；
（2）直线AB、CD是相交直线，点P是直线AB．CD外的一点，直线EF经过点P，且与直线AB平行，与直线CD相交于E．
如图所示，请画出下面实物的三视图：
画出图中的九块小立方块搭成几何体的主视图、左视图和俯视图．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网