题目内容
【题目】在直角三角形中,如果已知2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
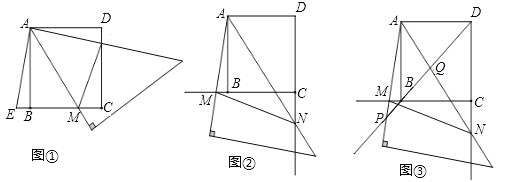
(1)观察下列4幅图,根据图中已知元素,可以求出其余未知元素的三角形是 .
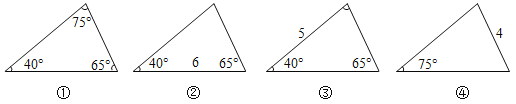
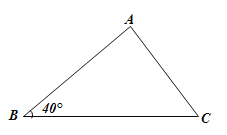
(2)如图,在△ABC中,已知∠B=40°,BC=18,AB=15,请求出AC的长度(答案保留根号).(参考数据:sin40°≈0.6,cos40°≈0.8,tan40°≈0.75)
【答案】(1)②,③;(2)![]()
【解析】
(1)①没有已知边,求不出边长,不合题意;②、③作出相应的垂线,根据锐角三角函数定义及勾股定理即可求出未知的元素,符合题意;④只知道一个角与一条边,求不出其他的角,不合题意,进而得出正确的选项;
(2)过A作AD垂直于BC,在直角三角形ABD中,由AB的长,利用锐角三角函数定义分别求出AD及BD的长,再由BCBD求出DC的长,在直角三角形ADC中,利用勾股定理即可求出AC的长.
解:(1)①没有已知边,求不出边长,不合题意;
②、③作出相应的垂线,根据锐角三角函数定义及勾股定理即可求出未知的元素,符合题意;④只知道一个角与一条边,求不出其他的角,不合题意,
故可以求出其余未知元素的三角形是②,③;
(2)如图,作AD⊥BC,D为垂足,
在Rt△ABD中,
∵sinB=![]() ,cosB=
,cosB=![]() ,AB=15,
,AB=15,
∴AD=ABsinB=15×0.6=9,BD=ABcosB=15×0.8=12,
∵BC=18,
∴CD=BCBD=1812=6,
则在Rt△ADC中,根据勾股定理得:AC=![]() .
.


练习册系列答案
相关题目