题目内容
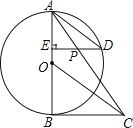
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF , 其中正确的结论有( )
S△ABF , 其中正确的结论有( )
A.5个
B.4个
C.3个
D.2个
【答案】B
【解析】解:过D作DM∥BE交AC于N,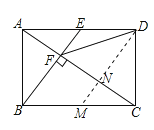
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
∵tan∠CAD=![]() ,
,
而CD与AD的大小不知道,
∴tan∠CAD的值无法判断,故④错误;
∵△AEF∽△CBF,
∴![]() ,
,
∴S△AEF=![]() S△ABF , S△ABF=
S△ABF , S△ABF=![]() S矩形ABCD
S矩形ABCD
∴S△AEF=![]() S矩形ABCD ,
S矩形ABCD ,
又∵S四边形CDEF=S△ACD﹣S△AEF=![]() S矩形ABCD﹣
S矩形ABCD﹣![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD ,
S矩形ABCD ,
∴S四边形CDEF=![]() S△ABF , 故⑤正确;
S△ABF , 故⑤正确;
所以正确的是:①②③⑤.
故选B.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分) | 人数(人) |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
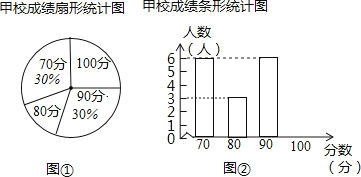
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
【题目】自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
选项 | 频数 | 频率 |
A | 30 | M |
B | n | 0.2 |
C | 5 | 0.1 |
D | 5 | 0.1 |

(1)这次被抽查的学生有多少人?
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?