题目内容
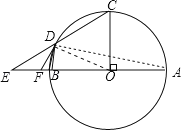
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
【答案】
(1)
【解答】证明:连结OD,如图,
∵CO⊥AB,
∴∠E+∠C=90°,
∵FE=FD,OD=OC,
∴∠E=∠FDE,∠C=∠ODC,
∴∠FDE+∠ODC=90°,
∴∠ODF=90°,
∴OD⊥DF,
∴FD是⊙O的切线;
(2)
解:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠A+∠ODB=90°,
∵∠BDF+∠ODB=90°,
∴∠A=∠BDF,
而∠DFB=∠AFD,
∴△FBD∽△FDA,
∴![]() ,
,
在Rt△ABD中,tan∠A=tan∠BDF=![]() ,
,
∴![]() ,
,
∴DF=2,
∴EF=2.

【解析】

练习册系列答案
相关题目