Question

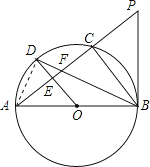
【题目】已知⊙O是以AB为直径的△ABC的外接圆，OD∥BC交⊙O于点D，交AC于点E，连接AD、BD，BD交AC于点F．

（1）求证：BD平分∠ABC；
（2）延长AC到点P，使PF=PB，求证：PB是⊙O的切线；
（3）如果AB=10，cos∠ABC=，求AD．

Answer 1

【答案】
（1）

【解答】证明：∵OD∥BC，

∴∠D=∠CBD，

∵OB=OD，

∴∠D=∠OBD，

∴∠CBD=∠OBD，

∴BD平分∠ABC；

（2）

证明：∵⊙O是以AB为直径的△ABC的外接圆，

∴∠ACB=90°，

∴∠CFB+∠CBF=90°．

∵PF=PB，

∴∠PBF=∠CFB，

由1知∠OBD=∠CBF，

∴∠PBF+∠OBD=90°，

∴∠OBP=90°，

∴PB是⊙O的切线；

（3）

解：连结AD．

∵在Rt△ABC中，∠ACB=90°，AB=10，

∴cos∠ABC=，

∴BC=6，AC==8．

∵OD∥BC，

∴△AOE∽△ABC，∠AED=∠OEC=180°﹣∠ACB=90°，

∴，，

∴AE=4，OE=3，

∴DE=OD﹣OE=5﹣3=2，

∴AD===．

【解析】（1）先由OD∥BC，根据两直线平行内错角相等得出∠D=∠CBD，由OB=OD，根据等边对等角得出∠D=∠OBD，等量代换得到∠CBD=∠OBD，即BD平分∠ABC；
（2）先由圆周角定理得出∠ACB=90°，根据直角三角形两锐角互余得到∠CFB+∠CBF=90°．再由PF=PB，根据等边对等角得出∠PBF=∠CFB，而由（1）知∠OBD=∠CBF，等量代换得到∠PBF+∠OBD=90°，即∠OBP=90°，根据切线的判定定理得出PB是⊙O的切线；
（3）连结AD．在Rt△ABC中，由cos∠ABC=，求出BC=6，根据勾股定理得到AC==8．再由OD∥BC，得出△AOE∽△ABC，∠AED=∠OEC=180°﹣∠ACB=90°，根据相似三角形对应边成比例求出AE=4，OE=3，那么DE=OD﹣OE=2，然后在Rt△ADE中根据勾股定理求出AD==2．