��Ŀ����
����Ŀ����֪��OΪ��ABC�����Բ��Բ��O��AB�ϣ� SA'>�����ԣ�����Ϊ�����ݹ���ÿһ������Ե�10�֣��������20�֣��������÷�Ҳ���۷֣�
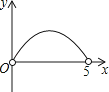
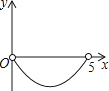
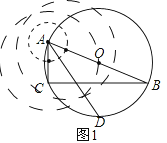
��1����ͼ1�У��ó߹���ͼ����BAC��ƽ����AD����O��D��������ͼ�ۼ�����д������֤������
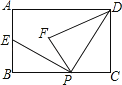
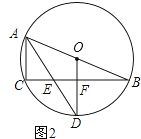
��2����ͼ2�����BAC��ƽ����AD��BC��E����O�뾶Ϊ5��AC=4������OD��BC��F������֤��OD��BC������EF�ij���
���𰸡�
��1��
�⣺�߹���ͼ��ͼ1��ʾ��
��2��
�⣺����ͼ2����ADƽ�֡�BAC��
���DAC=��BAD��
��OA=OD��
���OAD=��D��
���CAD=��D��
��AC��OD��
���ACB=��OFB��
��AB��ֱ����
���ACB=90�㣬
���OFB=90�㣬
��OD��BC��
�ڡ�AC��OD��
��![]() ����
����![]() ��
��
��OF=2��
��FD=5��2=3��
��RT��OFB��BF=![]() ��
��
��OD��BC��
��CF=BF=![]() ��
��
��AC��OD��
���EFD�ס�ECA��
��![]() ��
��
��![]() ��
��
��EF=![]() CF=
CF=![]() ��
��![]() =
=![]() ��
��
����������1����������ƽ���ߵķ����������ɣ�
��2���������AC��OD��Ȼ�����Բ�ܽǶ�����á�ACB=90�㣬����֤�ã��ڸ��ݹ��ɶ������BF����CF�ij���Ȼ�����ƽ���߷��߶γɱ����������![]() ���������
���������![]() ���̶����EF�ij���
���̶����EF�ij���
�����㾫�������չ��ɶ����ĸ����Բ�ܽǶ����ǽ����ĸ�������Ҫ֪��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��������Բ���ϵĽǽ���Բ�Ľ�;������Բ���ϣ����������߷ֱ���Բ����һ������Ľǽ���Բ�ܽ�;һ�������Ե�Բ�ܽǵ��������Ե�Բ�Ľǵ�һ�룮

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�