题目内容
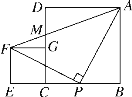
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
【答案】D
【解析】
①由同角的余角相等可证出△EPF≌△BAP,由此即可得出EF=BP,再根据正方形的性质即可得出①成立;②没有满足证明AP=AM的条件;③根据平行线的性质可得出∠GFP=∠EPF,再由∠EPF=∠BAP即可得出③成立;④在Rt△ABP中,利用勾股定理即可得出④成立;⑤结合④即可得出⑤成立.综上即可得出结论.
①∵∠EPF+∠APB=90°,∠APB+∠BAP=90°,
∴∠EPF=∠BAP.
在△EPF和△BAP中,有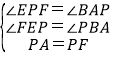 ,
,
∴△EPF≌△BAP(AAS),
∴EF=BP,
∵四边形CEFG为正方形,
∴EC=EF=BP,即①成立;
②无法证出AP=AM;
③∵FG∥EC,
∴∠GFP=∠EPF,
又∵∠EPF=∠BAP,
∴∠BAP=∠GFP,即③成立;
④由①可知EC=BP,
在Rt△ABP中,AB2+BP2=AP2,
∵PA=PF,且∠APF=90°,
∴△APF为等腰直角三角形,
∴AF2=AP2+EP2=2AP2,
∴AB2+BP2=AB2+CE2=AP2=![]() AF2,即④成立;
AF2,即④成立;
⑤由④可知:AB2+CE2=AP2,
∴S正方形ABCD+S正方形CGFE=2S△APF,即⑤成立.
故成立的结论有①③④⑤.
故选D.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目