题目内容
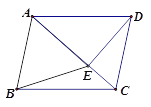
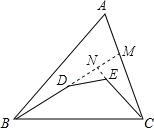
【题目】已知:如图,在△ABC中有D、E两点,求证:BD+DE+EC<AB+AC.

【答案】见解析
【解析】试题分析:延长BD交AC于M点,延长CE交BD的延长线于点N.在△ABM中,AB+AM>BM,在△CNM中,NM+MC>NC,所以AB+AM+NM+MC>BM+NC,再由AM+MC=AC,BM=BN+NM可知AB+AC+NM>BN+NM+NC,故AB+AC>BN+NC,在△BNC中,BN+NC=BD+DN+NE+EC,在△DNE中,DN+NE>DE,由此即可得出结论.
试题解析:延长BD交AC于M点,延长CE交BD的延长线于点N.
在△ABM中,AB+AM>BM,
在△CNM中,NM+MC>NC,
∴AB+AM+NM+MC>BM+NC,
∵AM+MC=AC,BM=BN+NM,
∴AB+AC+NM>BN+NM+NC,
∴AB+AC>BN+NC①
在△BNC中,BN+NC=BD+DN+NE+EC,②
在△DNE中,DN+NE>DE③
由②、③得:BN+NC>BD+DE+EC④
由①、④得:AB+AC>BN+NC>BD+DE+EC.
即:BD+DE+EC<AB+AC.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目