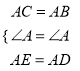题目内容
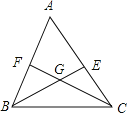
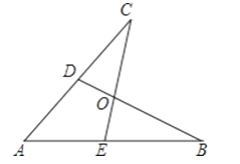
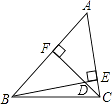
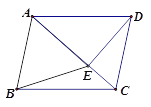
【题目】如图,在四边形ABCD中,AB//CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE .
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长 .
,求对角线AC的长 .
【答案】(1)证明见解析;(2)BE⊥AC,理由见解析;(3)AC=![]()
【解析】试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;(2)求出AD=DC,根据菱形的判定得出四边形ABCD是菱形,根据等腰三角形的性质得出即可;(3)根据等边三角形的性质得出AB=AE,∠BAC=60°,求出∠DCE=∠BAE=60°,求出CD=2EC,设CE=x,则AB=DC=AE=2x,根据勾股定理得出方程,求出x,即可得出答案.
试题解析:(1) 证明:∵AB∥CD
∴∠ABC+∠BCD=180°,
∠ADC+∠BAD=180°,
又∵∠ABC =∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形.
(2)∵DE⊥AC,且E是AC的中点,
∴ AD=DC .
由(1)可得四边形ABCD是平行四边形
∴ 四边形 ABCD是菱形.
∴ AB=BC
∵ E是AC中点,
∴ BE⊥AC.
(3)在平行四边形ABCD中,AB∥CD
∵△ABE是等边三角形
∴ ∠BAE=60°
∴ ∠ACD=60°
∵ DE⊥AC
∴ ∠DEC=90°,
∴ ∠EDC=30° ,
∴ EC=![]() DC
DC
设EC=x,则DC=2x
∴ DE=![]() , AB=AE=2x ,
, AB=AE=2x ,
在Rt△ADE中,
AE2+OE2=AD2
∴![]() , 解得
, 解得 ![]() ,
,
∴AC=3![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目