题目内容
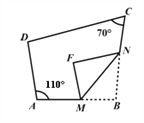
【题目】如图，四边形ABCD中，点M、N分别在AB、BC上，将BMN沿MN翻折，得FMN，若MF∥AD，FN∥DC，则∠D的度数为_________
【答案】90
【解析】首先利用平行线的性质得出∠BNF=100°，∠FNB=70°，再利用翻折变换的性质得出∠FMN=∠BMN=50°，∠FNM=∠MNB=35°，进而求出∠B的度数以及得出∠D度数.
解：∵MF∥AD，FN∥DC，∠A=100°，∠C=70°，
∴∠BMF=100°，∠FNB=70°，
∵将△BMN沿MN翻折，得△FMN，
∴∠FMN=∠BMN=50°，∠FNM=∠MNB=35°，
∴∠F=∠B=180°-50°-35°=95°
∴∠D=360°-100°-70°-90°=95°.
“点睛”此题主要考查了平行线的性质以及多边形内角和定理以及翻折变换的性质，得出∠FMN=∠BMN，∠FNM=∠MNB是解题关键.
练习册系列答案
相关题目
