题目内容
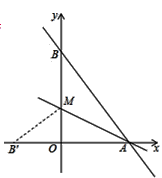
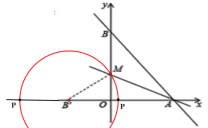
【题目】如图,直线y=-![]() x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
(1)求A、B两点的坐标;
(2)求直线AM的表达式;
(3)在x轴上是否存在点P,使得以点P、M、B′为顶点的三角形是等腰二角形,若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(4,0)或
;(3)P(4,0)或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)求点A坐标,令y=0,得A点坐标(6,0),求点B坐标,令x=0,得A点坐标(0,8);(2)由勾股定理可得线段AB=10,由折叠的性质可知![]() ,设
,设![]() ,在
,在![]() 中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
解:(1)y=-![]() x+8
x+8
令![]() 则
则![]() ,
,
令![]() ,则
,则![]()
![]()
(2)由(1)知![]() ,由勾股定理得
,由勾股定理得![]() ,
,
由折叠的性质可知![]() ,
,
设![]() ,则
,则![]()
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
解得 ![]()
![]()
设直线AM的表达式为![]()
则![]() ,解得
,解得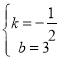
所以直线AM的表达式为![]() .
.
(3)由(2)知![]() ,可得
,可得![]()
①以点M为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
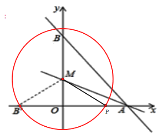
可得![]() ,所以P(4,0);
,所以P(4,0);
②以点![]() 为圆心,
为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
![]() 或1,所以
或1,所以![]() 或
或![]() ;
;
作线段![]() 的垂直平分线交x轴于一点P,此时
的垂直平分线交x轴于一点P,此时![]()
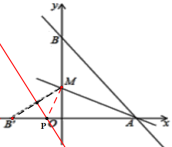
设![]() ,则
,则 ![]() ,根据勾股定理得
,根据勾股定理得![]() ,解得
,解得![]()
所以![]() .
.
综合上述,点P的坐标为P(4,0)或![]() 或
或![]() 或
或![]()

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
乙种节能灯 | 35 | 50 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完100只节能灯后,该商场获利多少元?