Question

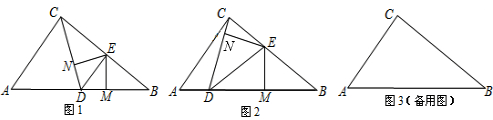
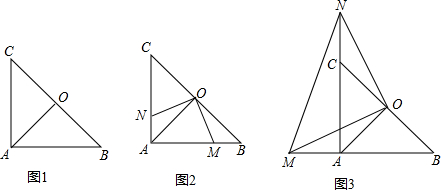
如图1，在Rt△ABC中，AB=AC，∠BAC=90°，点O是BC的中点，连接OA．
（1）OA=OB=OC成立吗？请说明理由．
（2）如图2，若点M，N分别在线段AB，AC上移动，在移动中始终保持AN=BM，△OAN≌△OBM成立吗？，并说明理由．
（3）如图3，若点M，N分别在线段BA．AC的延长线上移动，在移动中始终保持AN=BM，请判断△OMN的形状，并说明理由．

Answer 1

分析：（1）根据等腰直角三角形的性质得出AO=

1

2

BC进而得出OA=OB=OC；
（2）利用等腰直角三角形的性质得出∠B=∠OAN=45°，AO=BO，进而得出答案；
（3）利用等腰直角三角形的性质得出∠B=∠OAN=45°，AO=BO，进而得出△OAN≌△OBM，△OMN是等腰直角三角形．

解答：解：（1）成立．
理由：∵点O是BC的中点
∴BO=CO=

1

2

BC，
∵∠BAC=90°
∴AO=

1

2

BC，
∴OA=OB=OC；

（2）成立．
理由：∵O是BC的中点
∴AO是Rt△ABC的BC边上的中线
又∵AB=AC，
∴AO⊥BC，AO平分∠BAC，
∴∠B=∠OAN=45°，AO=BO，
∵在△OAN和△OBM中，

AN=BM ∠NAO=∠B AO=BO

，
∴△OAN≌△OBM（SAS）；

（3）△OMN是等腰直角三角形；
理由：∵O是BC的中点
∴AO是Rt△ABC的BC边上的中线
又∵AB=AC，
∴AO⊥BC，AO平分∠BAC，
∴∠B=∠OAN=45°，AO=BO，
∵AN=BM，
∴AN=BM，
∵在△OAN和△OBM中，

AN=BM ∠NAO=∠B AO=BO

，
∴△OAN≌△OBM（SAS）；
∴OM=ON，∠AOM=CON，
∴∠MON=∠MOC+∠CON=∠MOC+∠AOM=∠AOC=90°，
∴△OMN是等腰直角三角形．

点评：此题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质，根据已知得出△OAN≌△OBM是解题关键．