题目内容
如图1,在Rt△ABC中,AB=AC=3,BD为AC边的中线,AB1⊥BD交BC于B1,B1A1⊥AC于A1.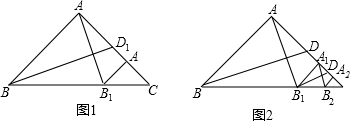
(1)求AA1的长;
(2)如图2,在Rt△A1B1C中按上述操作,则AA2的长为
(3)在Rt△A2B2C中按上述操作,则AA3的长为
(4)一直按上述操作得到Rt△An-1Bn-1C,则AAn的长为
分析:(1)根据等角的余角相等,得∠A1AB1=∠ABD,从而根据两角对应相等,证明△A1AB1∽△ABD.设A1A=x,则A1B1=A1C=3-x,根据相似三角形的性质即可求解.
(2)根据(1)的求解过程,易知A1A2是1的
,从而求解;
(3)、(4)根据(1)、(2)的结论,即可推而广之.
(2)根据(1)的求解过程,易知A1A2是1的
| 2 |
| 3 |
(3)、(4)根据(1)、(2)的结论,即可推而广之.
解答:解:(1)∵在Rt△ABC中,AB=AC=3,BD为AC边的中线,
∴AD=
.
∵在Rt△ABC中,AB1⊥BD,
∴∠A1AB1=∠ABD,
∴△A1AB1∽△ABD.
根据题意,易知△A1B1C是等腰直角三角形.
设A1A=x,则A1B1=A1C=3-x,
∴
=
,
即
=
,
解得x=2.
即AA1=2.
(2)根据(1)的求解过程,得A1A2=
,
则AA2=
.
(3)根据(2)、(3)的结论,推而广之,则AAn=
.
∴AD=
| 3 |
| 2 |
∵在Rt△ABC中,AB1⊥BD,
∴∠A1AB1=∠ABD,
∴△A1AB1∽△ABD.
根据题意,易知△A1B1C是等腰直角三角形.
设A1A=x,则A1B1=A1C=3-x,
∴
| AA1 |
| A1B1 |
| AB |
| AD |
即
| x |
| 3-x |
| 3 | ||
|
解得x=2.
即AA1=2.
(2)根据(1)的求解过程,得A1A2=
| 2 |
| 3 |
则AA2=
| 8 |
| 3 |
(3)根据(2)、(3)的结论,推而广之,则AAn=
| 3n-1 |
| 3n-1 |
点评:此题主要考查了相似三角形的判定和性质、等腰三角形的性质,要求学生能够从已知的式子中找出规律.能够从特殊到一般推而广之

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目