题目内容
如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.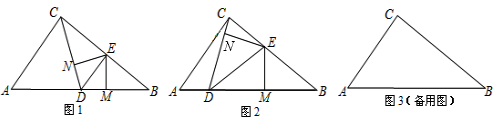
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,△BME与△CNE相似?
(3)探究:AD为何值时,四边形MEND与△BDE的面积相等?
分析:(1)由相似三角形的判定得出△DEB∽△ACB,从而得出角的关系,再由AD=CD,得出BD与AB的关系,即可求的结论.
(2)此题分两种情况求解,△BME∽△CNE或△BME∽△ENC,根据相似三角形的性质即可求得;
(3)根据四边形的面积求解方法,利用分割法求不规则四边形的面积,作辅助线EN⊥BD即可求得.
(2)此题分两种情况求解,△BME∽△CNE或△BME∽△ENC,根据相似三角形的性质即可求得;
(3)根据四边形的面积求解方法,利用分割法求不规则四边形的面积,作辅助线EN⊥BD即可求得.
解答:(1)证明:∵AD=CD
∴∠DAC=∠DCA
∴∠BDC=2∠DAC
∵DE是∠BDC的平分线
∴∠BDC=2∠BDE
∴∠DAC=∠BDE
∴DE∥AC;
(2)解:(I)当△BME∽△CNE时,得∠MBE=∠NCE
∴BD=DC
∵DE平分∠BDC
∴DE⊥BC,BE=EC
又∠ACB=90°
∴DE∥AC
∴
=
即BD=
AB=
=5
∴AD=5
(II)当△BME∽△ENC时,得∠EBM=∠CEN
∴EN∥BD
∵EN⊥CD
∴BD⊥CD即CD是△ABC斜边上的高
由三角形面积公式得AB•CD=AC•BC
∴CD=
∴AD=
=
综上,当AD=5或
时,△BME与△CNE相似;
(3)解:由角平分线性质易得S△MDE=S△DEN=
DM•ME
∵S四边形MEND=S△BDE
∴
BD•EM=DM•EM即DM=
BD
∴EM是BD的垂直平分线
∴BE=DE,DM=BM,
∴BD=2BM,
∴∠EDB=∠DBE
∵∠EDB=∠CDE
∴∠DBE=∠CDE
∵∠DCE=∠BCD
∴△CDE∽△CBD
∴
=
①,
∴
=
=
∵BC=8,
即CD=
∴cosB=
=
∴CD=4×
=5
由①式得CE=
=
∴BE=
∴BM=BE•cosB=
×
=
∴AD=AB-2BM=10-2×
=
.
∴∠DAC=∠DCA
∴∠BDC=2∠DAC
∵DE是∠BDC的平分线
∴∠BDC=2∠BDE
∴∠DAC=∠BDE
∴DE∥AC;
(2)解:(I)当△BME∽△CNE时,得∠MBE=∠NCE
∴BD=DC
∵DE平分∠BDC
∴DE⊥BC,BE=EC
又∠ACB=90°
∴DE∥AC
∴
| BE |
| BC |
| BD |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
∴AD=5
(II)当△BME∽△ENC时,得∠EBM=∠CEN
∴EN∥BD
∵EN⊥CD
∴BD⊥CD即CD是△ABC斜边上的高
由三角形面积公式得AB•CD=AC•BC
∴CD=
| 24 |
| 5 |
∴AD=
| AC2-CD2 |
| 18 |
| 5 |
综上,当AD=5或
| 18 |
| 5 |
(3)解:由角平分线性质易得S△MDE=S△DEN=
| 1 |
| 2 |
∵S四边形MEND=S△BDE
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴EM是BD的垂直平分线
∴BE=DE,DM=BM,
∴BD=2BM,
∴∠EDB=∠DBE
∵∠EDB=∠CDE
∴∠DBE=∠CDE
∵∠DCE=∠BCD
∴△CDE∽△CBD
∴
| CD |
| BC |
| CE |
| CD |
∴
| CD |
| BC |
| BE |
| BD |
| BE |
| 2BM |
∵BC=8,
即CD=
| 4BE |
| BM |
∴cosB=
| BM |
| BE |
| 4 |
| 5 |
∴CD=4×
| 5 |
| 4 |
由①式得CE=
| CD2 |
| BC |
| 25 |
| 8 |
∴BE=
| 39 |
| 8 |
∴BM=BE•cosB=
| 4 |
| 5 |
| 39 |
| 8 |
| 39 |
| 10 |
∴AD=AB-2BM=10-2×
| 39 |
| 10 |
| 11 |
| 5 |

点评:此题考查了平行线的判定,还考查了相似三角形的判定与性质,解题时要注意数形结合思想的应用,要注意不规则图形的面积的求解方法.

练习册系列答案
相关题目