题目内容
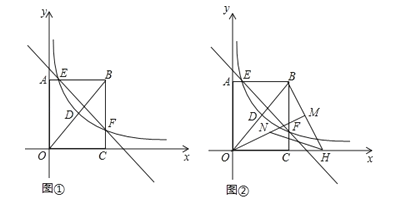
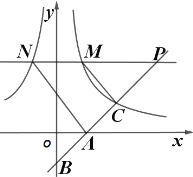
【题目】如图,已知正比例函数和反比例函数的图像都经过点![]() ,且
,且![]() 为双曲线上的一点,
为双曲线上的一点,![]() 为坐标平面上一动点,
为坐标平面上一动点,![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别是
轴,垂足分别是![]() 、
、![]() .
.
(1)写出正比例函数和反比例函数的关系式.
(2)当点![]() 在直线
在直线![]() 上运动时,直线
上运动时,直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 与
与![]() 的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
【答案】(1)正比例函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ;
;
(2)在直线![]() 上存在这样的点
上存在这样的点![]() 或
或![]() ,使得
,使得![]() 与
与![]() 面积相等.
面积相等.
【解析】
(1)用待定系数法进行求解,即可得到正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,![]() x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0,![]() x).根据三角形的面积公式列出关于x的方程,解方程即可.
x).根据三角形的面积公式列出关于x的方程,解方程即可.
(1)设反比例函数的解析式为![]() ,正比例函数的解析式为
,正比例函数的解析式为![]() .
.
∵正比例函数和反比例函数的图像都经过点![]() ,∴
,∴![]() ,
,![]() . ∴
. ∴![]() ,
,![]() .
.
∴正比例函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() .
.
(2)当点![]() 在直线
在直线![]() 上运动时,假设在直线
上运动时,假设在直线![]() 上存在这一的点
上存在这一的点![]() ,使得
,使得![]() 与
与![]() 面积相等,则
面积相等,则![]() .
.
∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() . 当
. 当![]() 时,
时,![]() .
.
故在直线![]() 上存在这样的点
上存在这样的点![]() 或
或![]() ,使得
,使得![]() 与
与![]() 面积相等.
面积相等.

练习册系列答案
相关题目