题目内容
【题目】综合题
（1）【结论再现】如图①，在 
中， 
， 
，则 
， 
． 
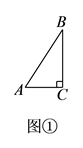
（2）【问题解决】
如图②，四边形 
是一张边长为 
的正方形纸片， 
、 
分别为 
、 
的中点，沿过点 
的折痕将纸片翻折，使点 
落在 
上的点 
处，折痕交 于点 
，求 
的度数和 
的长．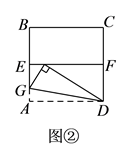
（3）【问题探究】
如图③，点 是等腰 斜边 
所在直线上一点，且满足 
，求 
的大小和此时 
的值．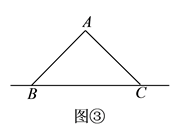
【答案】
（1）解： 
,
（2）解：∵ 
折叠后得到 
，
∴ 
，且 
，
∴在 
中， 
，sin∠FA′D= 
= 
，
∴ 
，
∴ 
，
在 
中， 
，
∴ 
，
又∵在 
中， 
，那么 
，
∴ 
，
∴ 
，
则 
，
那么 
（3）解：如图，
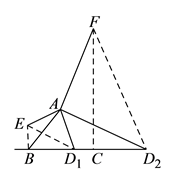
①当 
在 
边上时，将线段 
绕点 
顺时针方向旋转 
得到线段 
，连接 
，
与（1）同理可证 
≌ 
，
∴ 
， 
，
∵ 
，∴ 
，
∴ 
，
∴ 
，
∵ 
,
∴四边形 ． 
、 
． 
四点共圆，
∴ 
，
∴ 
．
②当 在 延长线上时，将线段 
绕点 逆时针方向旋转 得到线段 
，连接 
．
同理可证： 
，
∵ 
,∴四边形 ． 
． 
、 
四点共圆，∴ 
，
∴ 
，
综上， 
的度数为 
或 
．
比值计算如下：
过点 作 
，如图，
则在 
中， 
， 
，∴ 
， 
，
在 
中， 
，
设 
， 
，∴ 
，
∴ 
，
∴ 
．
【解析】（1）利用锐角三角函数的定义及特殊角的三角函数值，即可求出∠B的度数及
的值。
（2）根据折叠的性质先求出∠FAD、∠EA′G的度数，再利用勾股定理在Rt△A′FD中求出A′F的长，即可得出A′E的长，再利用直角三角形的性质得出A′G的长，然后求出EG的长，从而得到BG的长。
（3）根据题意画出图形，分两种情况讨论：①当 D 在 B C 边上时，将线段 A D 1 绕点 A 顺时针方向旋转 90 ° 得到线段 AE ，连接 BE ，先证明△ABE ≌ △ACD1 ，根据全等三角形的性质及特殊角的三角函数值求出 ∠BD1E=30°，得到四边形 A ． D1 、 B ． E 四点共圆，然后根据圆周角定理即可求出结果；②当 D 在 B C 延长线上时，将线段 A D 绕点 A 逆时针方向旋转 90 ° 得到线段 A F ，连接 C F ．同①的方法类似求出结果即可，根据锐角三角函数的定义得出AD=
,再求出ED的长，然后根据AD=
x，即可求出结果。
