题目内容
【题目】已知一次函数
的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．
（1）求点B的坐标；
（2）求直线AE的表达式；
（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．
（4）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．
【答案】（1）B（8，0）；（2）y=﹣2x+6；（3）△OFB为等腰三角形，S△OBF=8； （4）y=
（0＜x＜8）．
【解析】试题分析: （1）如图1中，设OE=x，作EM⊥AB于M．首先证明△AEO≌△AEM，推出AM=AO=6，由OA=6，OB=8，∠AOB=90°，推出AB=10，推出BM=4，在Rt△EBM中，根据EM2+BM2=EB2，可得x2+42=（8-x）2，解方程即可．
（2）根据S△AEB= 
，即可解决问题．
（3）利用面积即可解决，方法类似（2）．
试题解析: （1）如图1中，
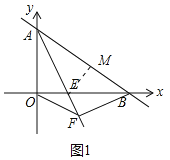
∵一次函数y=-
x+6的图象与坐标轴交于A、B点，
∴A（0，6），B（8，0），设OE=x，作EM⊥AB于M．
∵AE平分∠OAB，OE⊥OA，
∴OE=EM=x，
在△AEO和△AEM中，
，
∴△AEO≌△AEM，
∴AM=AO=6，
∵OA=6，OB=8，∠AOB=90°，
∴AB=10，
∴BM=4，
在Rt△EBM中，∵EM2+BM2=EB2，
∴x2+42=（8-x）2，
∴x=3，
∴E（3，0），
设直线AE的解析式为y=kx+b则
，解得
，
∴直线AE的解析式为y=-2x+6．
（2）由（1）可知OE=3，AE=
，EB=5，
∵S△AEB=
EBOA=
AEBF，
∴BF=
．
（3）如图2中，
在Rt△AOE中， 
，
∴AE=
，
∵S△AEB=
EBOA=
AEBF
∴BF=
，
∴y=
（0＜x＜8）．
