题目内容
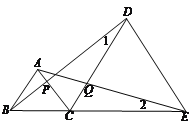
【题目】线段BE上有一点C，以BC，CE为边分别在BE的同侧作等边三角形ABC，DCE，连接AE，BD，分别交CD，CA于Q，P.
（1）找出图中的所有全等三角形.
（2）找出一组相等的线段，并说明理由.
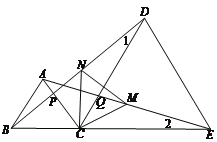
（3）取AE的中点M、BD的中点N，连接MN，试判断三角形CMN的形状，并说明理由.
【答案】（1）△BCD≌△ACE；△BPC≌ △AQC； △DPC≌△EQC；（2）BD=AE，理由见解析；（3）等边三角形，理由见解析.
【解析】（1）△BCD≌△ACE；△BPC≌ △AQC；△DPC≌△EQC.
（2）BD=AE．理由如下：
等边三角形ABC、DCE中，∵∠ACB=∠ACD=∠DCE=60°，∴∠BCD=∠ACE，
在△BCD和△ACE中，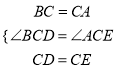 
，∴△BCD≌△ACE（SAS），∴BD=AE．
（3）等边三角形，理由如下：
由△BCD≌△ACE，可得∠1=∠2，BD=AE，M是AE的中点、N是BD的中点，
∴DN=EM，又DC=CE，在△DCN和△ECM中，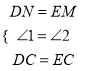 
，∴△DCN≌△ECM（SAS），
∴CN=CM，∠NCD=∠MCE，∠MCE+∠DCM=60°，所以∠NCD+∠DCM=60°，即∠NCM=60°，∴△CMN为等边三角形．
练习册系列答案
相关题目
