Question

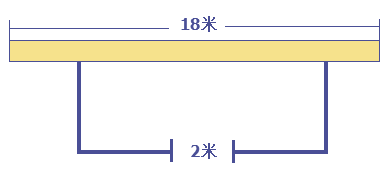
【题目】邻居张老汉养了一群鸡，现在要建一长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边（门除外）用竹篱笆围成，篱笆总长34米．请同学解决以下问题：

（1）若设鸡场的面积为y平方米，鸡场与墙平行的一边长为x米，请写出y与x之间的函数关系式，并写出x的取值范围；

（2）当鸡场的面积为160平方米时，鸡场的长与宽分别是多少米？

（3）鸡场的最大面积是多少？并求出此时鸡场的长与宽分别是多少米？

Answer 1

【答案】（1）y= -x2+18x（2<x≤18）；（2）鸡场的长与宽分别为16米、10米；（3）鸡场的最大面积为162平方米，此时鸡场的长与宽分别为18米、9米．

【解析】

（1）用含x的式子表示鸡场与墙垂直的一边长，根据矩形面积公式即可写出函数关系式；
（2）根据（1）所得关系式，将y=160代入即可求解；
（3）求出函数的最大值，使得面积取最大值即可求解．

解：（1）根据题意，鸡场与墙平行的一边长为x米，可得鸡场与墙垂直的一边长为米，即（18-）米，

可得y=x（18-）= -x2+18x（2<x≤18）；

（2）令y=160，即-x2+18x=160，

解得x1=16，x2=20（不合题意，舍去），所以x=16．

当x=16时，18-=10．

所以，鸡场的长与宽分别为16米、10米；

（3）对于y== -x2+18x，a= -<0，所以函数有最大值， 当x= -=18时，函数有最大值，最大值y=162

当x=18时，18-=9．

所以鸡场的最大面积为162平方米，此时鸡场的长与宽分别为18米、9米．