题目内容
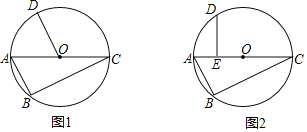
【题目】已知,如图1,⊙O是四边形ABCD的外接圆,连接OC交对角线BD于点F,延长AO交BD于点E,OE=OF.
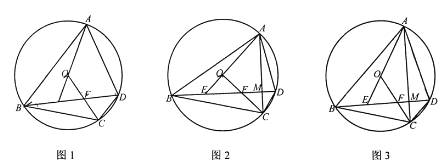
(1)求证:BE=FD;
(2)如图2,若∠EOF=90°,BE=EF,⊙O的半径![]() ,求四边形ABCD的面积;
,求四边形ABCD的面积;
(3)如图3,若AD=BC;
①求证:![]() ;②若
;②若![]() ,直接写出CD的长.
,直接写出CD的长.
【答案】(1)见详解;(2)12![]() ;(3)①见详解,②3
;(3)①见详解,②3![]() -
-![]()
【解析】
(1)如图1中,作OH⊥BD于H.根据等腰三角形的性质以及垂径定理即可;
(2)如图2中,作OH⊥BD于H,连接OB,求出AC,BD,根据S四边形ABCD=![]() BDAM+
BDAM+
![]() BDCM=
BDCM=![]() BDAC即可求解;
BDAC即可求解;
(3)①如图3中,连接OB,作OH⊥BD于H.利用等腰直角三角形的性质,完全平方公式等知识即可;
②如图3中,连接OB,设DM=CM=x,想办法求出BC,DB,在Rt△BCM中,利用勾股定理构建方程即可.
(1)证明:如图1中,作OH⊥BD于H.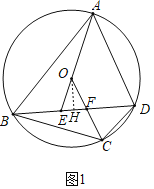
∵OE=OF,OH⊥EF,
∴EH=HF,
∵OH⊥BD,
∴BH=HD,
∴BE=DF;
(2)解:如图2中,作OH⊥BD于H,连接OB.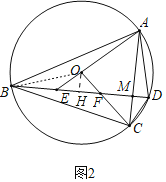
∵∠EOF=90°,OE=OF,OA=OC,
∴∠OEF=∠OAC=45°,
∴∠AME=90°,即AC⊥BD,
连接OB.设OH=a,
∵BE=EF,
∴BE=2EH=2OH=2a,
在Rt△BOH中,∵OH2+BH2=OB2,
∴a2+(3a)2=(2![]() )2,
)2,
∴a=![]() 或-
或-![]() (舍弃),
(舍弃),
∴BD=BE+EF+DF=6a=6![]() ,
,
在Rt△AOC中,AC=![]() AO=2
AO=2![]() ,
,
∴S四边形ABCD=![]() BDAM+
BDAM+![]() BDCM=
BDCM=![]() BDAC=
BDAC=![]() ×2
×2![]() ×6
×6![]() =12
=12![]() ;
;
(3)①如图3中,连接OB,作OH⊥BD于H.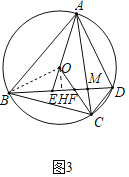
∵OE=OF,OA=OC,
∴∠EOH=![]() ∠EOF=
∠EOF=![]() (∠EAC+∠ACO)=
(∠EAC+∠ACO)=![]() ×2∠OAC=∠OAC,
×2∠OAC=∠OAC,
∴AC∥OH,
∴AC⊥BD,
∵AD=BC,
∴∠ABD=∠CAB=∠CDB=45°,
∴AB=![]() BM,CD=
BM,CD=![]() DM,CM=DM,
DM,CM=DM,
∴ABCD+BC2=![]() BM
BM![]() DM+BM2+CM2=(BM+DM)2=BD2;
DM+BM2+CM2=(BM+DM)2=BD2;
②如图3中,连接OB,设DM=CM=x,
∵∠BOC=2∠BDC=90°,
∴BC=![]() OB=2
OB=2![]() ,
,
∵ABCD+BC2=BD2,ABCD=AO2=12,
∴12+24=BD2,
∴BD=6(负根已经舍弃),
在Rt△BCM中,∵BC2=BM2+CM2,
∴(2![]() )2=(6-x)2+x2,
)2=(6-x)2+x2,
∴x=3-![]() 或3+
或3+![]() (舍弃),
(舍弃),
∴CD=![]() x=3
x=3![]() -
-![]() .
.

 名校课堂系列答案
名校课堂系列答案