题目内容
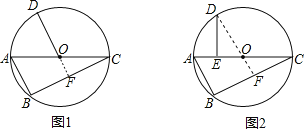
【题目】已知,△ABC内接于⊙O,AC为⊙O的直径,点D为优弧BC的中点
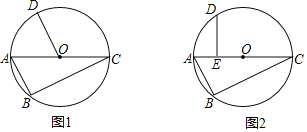
(1)如图1,连接OD,求证:AB∥OD;
(2)如图2,过点D作DE⊥AC,垂足为E.若AE=3,BC=8,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)如图1,延长DO交BC于F,根据垂径定理得到DF⊥BC,根据圆周角定理得到AB⊥BC根据平行线的判定定理即可得到AB∥OD;
(2)连接DO并延长交BC于F,由垂径定理得到DF⊥CB,求得CF=![]() BC=4,根据全等三角形的性质得到OF=OE=OA-3,根据勾股定理即可得到结论.
BC=4,根据全等三角形的性质得到OF=OE=OA-3,根据勾股定理即可得到结论.
(1)如图1,延长DO交BC于F,
∵点D为优弧BC的中点,
∴弧BD=弧CD,
∴DF⊥BC,
∵AC为⊙O的直径,
∴AB⊥BC,
∴AB∥OD;
(2)连接DO并延长交BC于F,
∵点D为优弧BC的中点,
∴弧BD=弧CD,
∴DF⊥CB,
∴CF=![]() BC=4,
BC=4,
∵DE⊥AC,
∴∠DEO=∠OFC=90°,
∵∠DOE=∠COF,OC=OD,
∴△DOE≌△COF(AAS),
∴OF=OE=OA-3,
∵OC2=OF2+CF2,
∴OC2=(OC-3)2+42,
∴OC=![]() ,
,
∴⊙O的半径为![]() .
.

练习册系列答案
相关题目