题目内容
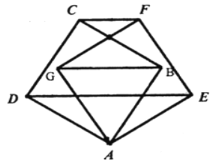
【题目】如图,正方形ABCD绕着点A顺时针旋转到正方形AEFG,连接CF、DE、GB,若DE=6,GB=4,则五边形AEFCD的面积为_____.
【答案】18
【解析】
过点E作DE的垂线,与DG的延长线相交于点K,设DK与CF相交于点M,证明△AED≌△FEK和△CDM≌△FKM,可得五边形AEFCD的面积=S△DEK,即可得出五边形AEFCD的面积.
解:如图,过点E作DE的垂线,与DG的延长线相交于点K,设DK与CF相交于点M,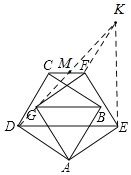
∵正方形ABCD绕着点A顺时针旋转到正方形AEFG,
∴AD=AG,
∴∠ADG=∠AGD=x,
∴∠DAG=180°-2x,
∵∠GAE=90°,DA=AB=AE,
∴∠DAE=270°-2x,
∴∠ADE=∠AED=[180°-(270°-2x)]÷2=x-45°,
∴∠GDE=x-(x-45°)=45°,
∴∠KDE=∠DKE=45°,
∴DE=KE,
∵AE=EF,∠DEK=∠AEF=90°,
∴∠AED=∠FEK,∠ADE=∠FKE,
∴△AED≌△FEK(SAS),
∴FK=AD=DC,
∵∠CDM=90°-45°-∠ADE=45°-∠ADE,∠FKM=45°-∠FKE,
∴∠CDM=∠FKM,
∵∠CMD=∠FMK,
∴△CDM≌△FKM(AAS),
∴五边形AEFCD的面积=S△DEK=![]() ×6×6=18.
×6×6=18.
故答案为:18.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目