��Ŀ����
����Ŀ����A��B��C�������ϱ�ʾ����a��b��c���㣨b+3��2+|c��24|=0���Ҷ���ʽx|a+3|y2��ax3y+xy2��1���������ʽ��
��1���ֱ���a��b��c��ֵ��
��2����֪��P����Q�������ϵ��������㣬��P�ӵ�A��������3����λ/����ٶ������˶���ͬʱ��Q�ӵ�C��������7����λ/����ٶ������˶���
������P�͵�Q����t����������ϵĵ�D�����������t��ֵ�͵�D����ʾ������
������P�˶�����B��������Q�ٳ�������P�˶������������֮��ľ���Ϊ5����λ��
���𰸡�
��1���⣺�ߣ�b+3��2+|c��24|=0��
��b=��3��c=24��
�߶���ʽx|a+3|y2��ax3y+xy2��1���������ʽ��
��|a+3|=5��2����a��0��
��a=��6��
�ʴ��ǣ���6����3��24
��2���⣺��������� 3t+7t=|��6��24|=30��
��� t=3��
��3t=9��
���ԩ�6+9=3��
���Գ�t��ֵ��3�͵�D����ʾ������3��
�����P�˶�x���P��Q�����ľ�����5��
����P�ڵ�Q�����ʱ��3x+5+7��x��1��=30��
��� x=3.2��
����P�ڵ�Q���ұ�ʱ��3x��5+7��x��1��=30��
��� x=4.2��
��������������P�˶�3.2���4.2���������֮��ľ���Ϊ5����λ��
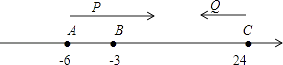
����������1�����÷Ǹ������������b��c��ֵ�����ݶ���ʽΪ�������ʽ���a��ֵ����2�������õ�P��Q���ߵ�·��=AC�г����̣��ڴ�����Ҫ�������ۣ�����ǰ�����������������PQ=5����Ҫ��ʱ�䣮

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�