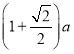题目内容
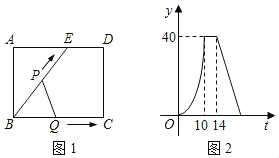
【题目】如图1，在矩形ABCD中，E是AD上的一点，点P从点B沿折线BE﹣ED﹣DC，运动到点C时停止；点Q从点B沿BC运动到点C时停止，速度均为每秒1个单位长度，如果点P，Q同时开始运动，设运动时间为t，△BPQ的面积为y，已知y与t的函数图象如图2所示，以下结论：①BC＝10； ②cos∠ABE＝
；③当t＝12时，△BPQ是等腰三角形；④当14≤t≤20时，y＝110﹣5t，其中正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】B
【解析】
由图象可知，当10≤t≤14时，y值不变，则此时，Q点到C，P从E到D．
得到BE＝BC＝10，ED＝4故可判断①，根据勾股定理求出AB，再根据cos∠ABE＝
求出，即可判断②，求出t＝12时，P在点E右侧2单位，利用勾股定理得到PC的长，即可判断③，当14≤t≤20时，点P由D向C运动，Q在C点，根据三角形的面积公式△BPQ的面积为
×10×（22﹣t）即可判断④.
解：由图象可知，当10≤t≤14时，y值不变，则此时，Q点到C，P从E到D．
∴BE＝BC＝10，ED＝4故①正确．
∴AE＝6，
Rt△ABE中，AB＝
，
∴cos∠ABE＝
故②错误；
t＝12时，P在点E右侧2单位，此时BP＞BE＝BC，
PC＝
，
∴△BPQ不是等腰三角形．故③错误；
当14≤t≤20时，点P由D向C运动，Q在C点，
△BPQ的面积为×10×（22﹣t）＝110﹣5t，则④正确．
∴正确的有①④共2个．
故选：B．
练习册系列答案
相关题目
