题目内容
【题目】已知PA与⊙O相切于点A,B、C是⊙O上的两点
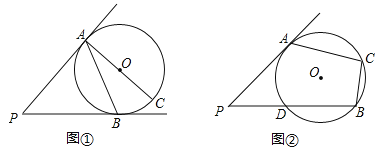
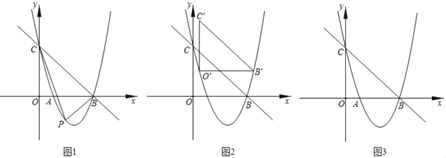
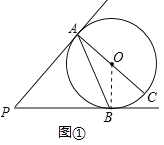
(1)如图①,PB与⊙O相切于点B,AC是⊙O的直径若∠BAC=25°;求∠P的大小
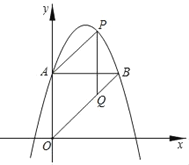
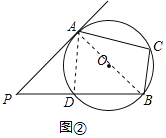
(2)如图②,PB与⊙O相交于点D,且PD=DB,若∠ACB=90°,求∠P的大小
【答案】(1)∠P=50°;(2)∠P=45°.
【解析】
(1)连接OB,根据切线长定理得到PA=PB,∠PAO=∠PBO=90°,根据三角形内角和定理计算即可;
(2)连接AB、AD,根据圆周角定理得到∠ADB=90°,根据切线的性质得到AB⊥PA,根据等腰直角三角形的性质解答.
解:(1)如图①,连接OB.
∵PA、PB与⊙O相切于A、B点,
∴PA=PB,
∴∠PAO=∠PBO=90°
∴∠PAB=∠PBA,
∵∠BAC=25°,
∴∠PBA=∠PAB=90°一∠BAC=65°
∴∠P=180°-∠PAB-∠PBA=50°;
(2)如图②,连接AB、AD,
∵∠ACB=90°,
∴AB是的直径,∠ADB=90·
∵PD=DB,
∴PA=AB.
∵PA与⊙O相切于A点
∴AB⊥PA,
∴∠P=∠ABP=45°.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目