题目内容
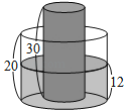
【题目】如图，有一内部装有水的直圆柱形水桶，桶高
；另有一直圆柱形的实心铁柱，柱高
，直立放置于水桶底面上，水桶内的水面高度为
，且水桶与铁柱的底面半径比为
．今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由水桶底面半径：铁柱底面半径=2：1，得到水桶底面积：铁柱底面积=4：1，设铁柱底面积为a(dm2)，水桶底面积为4a(dm2)，于是得到水桶底面扣除铁柱底面部分的环形区域面积为4a-a=3a(dm2)，，根据原有的水量为3a×12=36a (dm3)，列出方程，即可得到结论．
∵水桶底面半径：铁柱底面半径=2：1，
∴水桶底面积：铁柱底面积=4：1，
设铁柱底面积为a(dm2)，则水桶底面积为4a(dm2)，
∴水桶底面扣除铁柱底面部分的环形区域面积为4aa=3a(dm2)，
∴原有的水量为：3a×12=36a (dm3)，
设水桶内的水面高度变为xdm，
则4ax=36a，解得：x=9，
∴水桶内的水面高度变为9dm．
故选D．
练习册系列答案
相关题目
