题目内容
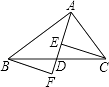
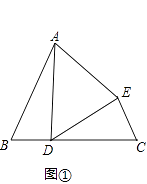
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
【答案】(1)证明见解析;(2)∠F=30°.
【解析】试题分析:连接OD,根据AB=AC得出∠ABC=∠ACB,根据OD=OC得出∠ODC=∠OCD,则∠ABC=∠ODC,从而得出AB∥OD,从而得到切线;连接AD,根据AC为直径得出AD⊥BC,根据DE⊥AB得出△AED和△ADB相似,根据半径得出AB、AC、AE、AD的长度,根据Rt△ADB的三角函数得出∠ABC的度数,从而得出∠F的度数.
试题解析:(1)证明:连接OD.∵AB=AC,∴![]() .∵OD=OC,∴
.∵OD=OC,∴![]() .
.
∴![]() .∴
.∴![]() ∥
∥![]() .∴
.∴![]() .∵DE⊥AB,∴
.∵DE⊥AB,∴![]() .
.
∴![]() .∴
.∴![]() .∴DE是⊙O的切线.
.∴DE是⊙O的切线.
解:连接AD.∵AC为⊙O的直径,∴![]() .
.
又∵DE⊥AB,∴Rt![]() ∽Rt
∽Rt![]() .∴
.∴![]() .∴
.∴![]() .
.
∵⊙O的半径为4,∴AB=AC=8.∴![]() . ∴
. ∴![]() .
.
在Rt![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
又∵AB=AC,∴![]() 是等边三角形.∴
是等边三角形.∴![]() ∴
∴![]() .
.

练习册系列答案
相关题目