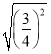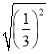题目内容
【题目】如图,在平面直角坐标系中,已知点A(﹣1,0),点B(3,0).在第三象限内有一点M(﹣2,m).
(1)请用含m的式子表示△ABM的面积;
(2)当m=-![]() 时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.

【答案】(1)-2m;(2)点P坐标是(0,﹣![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)过M作CE⊥x轴于E,根据点M在第三象限可得ME=-m,根据A、B坐标可求出AB的长,利用三角形面积公式即可得答案;(2)先根据(1)计算S△ABM,再分两种情况:当点P在y轴正半轴上时、当点P在y轴负半轴上时,利用割补法表示出S△BMP,根据S△BMP=S△ABM列方程求解可得.
(1)如图1所示,过M作CE⊥x轴于E,
∵A(﹣1,0),B(3,0),
∴OA=1,OB=3,
∴AB=4,
∵在第三象限内有一点M(﹣2,m),
∴ME=|m|=﹣m,
∴S△ABM=![]() AB×ME=
AB×ME=![]() ×4×(﹣m)=﹣2m;
×4×(﹣m)=﹣2m;
(2)当m=-![]() 时,M(-2,-
时,M(-2,-![]() )
)
∴S△ABM=-2×(-![]() )=3,
)=3,
点P有两种情况:
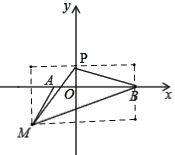
①当点P在y轴正半轴上时,设点p(0,k)
S△BMP=5×(![]() +k)-
+k)-![]() ×2×(
×2×(![]() +k)-
+k)-![]() ×5×
×5×![]() -
-![]() ×3×k=
×3×k=![]() k+
k+![]() ,
,
∵S△BMP=S△ABM,
∴![]() k+
k+![]() =3,
=3,
解得:k=![]() ,
,
∴点P坐标为(0,![]() );
);
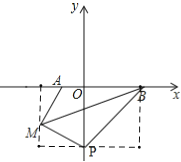
②当点P在y轴负半轴上时,设点p(0,n),
S△BMP=-5n-![]() ×2×(-n-
×2×(-n-![]() )-
)-![]() ×5×
×5×![]() -
-![]() ×3×(-n)=-
×3×(-n)=-![]() n-
n-![]() ,
,
∵S△BMP=S△ABM,
∴-![]() n-
n-![]() =3,
=3,
解得:n=﹣![]()
∴点P坐标为(0,﹣![]() ),
),
故点P的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).

练习册系列答案
相关题目