题目内容
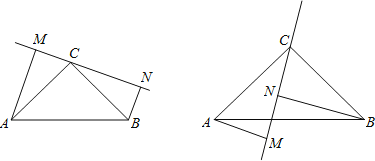
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A. 2018 B. 2017 C. 55 D. 45
【答案】D
【解析】
根据图形中的规律即可求出(a+b)10的展开式中第三项的系数.
找规律发现(a+b)3的第三项系数为3=1+2;
(a+b)4的第三项系数为6=1+2+3;
(a+b)5的第三项系数为10=1+2+3+4;
不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),∴(a+b)10第三项系数为1+2+3+…+9=45.
故选D.

【题目】为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:
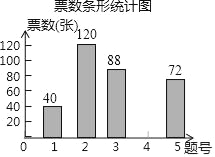
票数条形统计图
题目编号 | 人数 | 百分比 |
1 | 40 | 10% |
2 | 120 | m% |
3 | 88 | 22% |
4 | a | 20% |
5 | 72 | 18% |
合计 | 400 | 1 |
请根据图表提供的信息,解答下面问题:
(1)票数统计表中的a= ,m= .
(2)请把票数统计图补充完整;
(3)若绘制“票数扇形统计图”编号是“4”的题目所对应扇形的圆心角是 度;
(4)至本次投票结束,总票数共有1200票,请估计编号是“3”的题目约获得 票.
【题目】2019年暑假期间,某学校计划租用8辆客车送280名师生参加社会实践活动,现有甲、乙两种客车,它们的载客量和租金如表,设租用甲种客车x辆,租车总费用为w元.
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 40 |
租金(元/辆) | 270 | 320 |
(1)求出w(元)与x(辆)之间函数关系式,并直接写出自变量x的取值范围;
(2)选择怎样的租车方案所需的费用最低?最低费用多少元?