题目内容
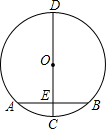
如图，AB为⊙O的直径，点C在⊙O上，∠BAC的平分线交BC于D，交⊙O于E，且AC=6，AB=8，求CE的长．
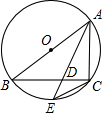
连接OE，
∵∠BAC的平分线交BC于D，
∴
=
，
∴BF=CF，
∵OA=OB，
∴OF是△ACB的中位线，
∴OF=
AC=
×6=3，
∴EF=1，
在Rt△OFB中，OB=
AB=4，
BF=
=
=
，
∴CF=
，
∴在Rt△EFC中，EC=
=
=2
．
∵∠BAC的平分线交BC于D，
∴
 |
| BE |
|
| CE |
∴BF=CF，
∵OA=OB，
∴OF是△ACB的中位线，
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=1，
在Rt△OFB中，OB=
| 1 |
| 2 |
BF=
| OB2-OF2 |
| 42-32 |
| 7 |
∴CF=
| 7 |
∴在Rt△EFC中，EC=
| EF2+CF2 |
12+(
|
| 2 |
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
