题目内容
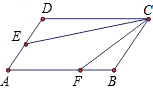
如图，正方形ABCD的边长为1，E是边CD上的一点，F是边CB延长线上的一点，如果△ADE∽△FCE∽△ABF，且∠DAE、∠CFE、∠BAF是对应角．求DE的长．
∵正方形ABCD的边长为1，
∴AD=AB=BC=CD=1，
∵△ADE∽△ABF，
∴
=
，
∴DE=BF，
设DE=x，
则BF=x，CE=CD-DE=1-x，CF=BC+BF=1+x，
∵△ADE∽△FCE，
∴
=
，
即
=
，
解得：x1=
-1，x2=-
-1（舍去），
∴DE=
-1．
∴AD=AB=BC=CD=1，
∵△ADE∽△ABF，
∴
| DE |
| BF |
| AD |
| AB |
∴DE=BF，
设DE=x，
则BF=x，CE=CD-DE=1-x，CF=BC+BF=1+x，
∵△ADE∽△FCE，
∴
| AD |
| FC |
| DE |
| CE |
即
| 1 |
| 1+x |
| x |
| 1-x |
解得：x1=
| 2 |
| 2 |
∴DE=
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
