题目内容
【题目】如图所示，在正方形ABCD中，点E是BC边上一点，且BE:EC=2：1，AE与BD交于点F，则△AFD与四边形DFEC的面积之比是________.
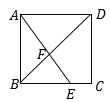
【答案】9:11
【解析】试题解析：设CE=x，S△BEF=a，
∵CE=x，BE：CE=2：1，
∴BE=2x，AD=BC=CD=AD=3x；
∵BC∥AD
∴∠EBF=∠ADF，
又∵∠BFE=∠DFA；
∴△EBF∽△ADF
∴S△BEF：S△ADF=（
）2=（
）2=
，那么S△ADF=
a．
∵S△BCD-S△BEF=S四边形EFDC=S正方形ABCD-S△ABE-S△ADF，
∴
x2-a=9x2-
×3x2x-
a，
化简可求出x2=
a；
∴S△AFD：S四边形DEFC=
a：（
x2-a）=
a： 
a =9：11．
练习册系列答案
名校课堂系列答案
相关题目
