题目内容
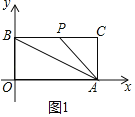
【题目】如图,在平面直角坐标系中,点A,B的坐标为(a,0),(0,b),且满足(a﹣4)2+![]() =0,现将OA平移到BC的位置,连接AC,点P从点B出发,沿BC﹣CA运动,速度为每秒1个单位长度,设运动时间为t秒.
=0,现将OA平移到BC的位置,连接AC,点P从点B出发,沿BC﹣CA运动,速度为每秒1个单位长度,设运动时间为t秒.
(1)求出a和b的值,并写出点C的坐标;
(2)求点P在运动过程中的坐标(用含t的式子表示).
(3)点Q以每秒3.5个单位长度的速度从点A出发,在AO间往返运动,(两个点同时出发,当点P到达点A停止时点Q也停止),在运动过程中,直接写出当PQ∥OB时,点P的坐标.
【答案】(1)a=4,b=2,(4,2);(2)(4,6﹣t);(3)点P的坐标为(![]() ,2)或(
,2)或(![]() ,2)或(
,2)或(![]() ,2)或(4,
,2)或(4,![]() )
)
【解析】
(1)根据非负数的性质求出a和b的值,进而得到点C的坐标;
(2)当t为0到4时,点P在线段BC上,易求其坐标;当t为4到6时,点P在线段CA上,易求其坐标;
(3)分两种情况:①点P在线段BC上,由于OQ∥BP,所以当OQ=BP时,四边形OBPQ是矩形,则有PQ∥OB.此时又分三种情况:Ⅰ)点Q的运动路线是A﹣O;Ⅱ)点Q的运动路线是A﹣O﹣A;Ⅲ)点Q的运动路线是A﹣O﹣A﹣O;②点P在线段CA上时,Q只能在A点,求出此时t的值,进而得到点P的坐标.
解:(1)∵(a﹣4)2+![]() =0,
=0,
∴a﹣4=0,2a﹣3b﹣2=0,
∴a=4,b=2,
∴点A,B的坐标分别为(4,0),(0,2),
∵四边形OACB是矩形,
∴点C的坐标是(4,2);
(2)∵点P为从B出发沿BC﹣CA运动的一动点,速度为每秒1个单位长度,设运动时间为t秒,
∴当t为0到4时,点P在线段BC上,BP=t,所以P点坐标可表示为(t,2),
当t为4到6时,点P在线段CA上,AP=6﹣t,所以P点坐标可表示为(4,6﹣t);
(3)分两种情况:
①点P在线段BC上时,BP=t,0≤t≤4,当OQ=BP时,PQ∥OB.
(Ⅰ)点Q的运动路线是A﹣O,
∵AQ=3.5t,
∴OQ=OA﹣AQ=4﹣3.5t,
∵OQ=BP,
∴4﹣3.5t=t,
解得:t=![]() ,
,
∴点P的坐标为(![]() ,2);
,2);
(Ⅱ)点Q的运动路线是A﹣O﹣A,
OQ=3.5t﹣4,
∵OQ=BP,
∴3.5t﹣4=t,
解得:t=![]() ,
,
∴点P的坐标为(![]() ,2);
,2);
(Ⅲ)点Q的运动路线是A﹣O﹣A﹣O,
OQ=12﹣3.5t,
∵OQ=BP,
∴12﹣3.5t=t,
解得:t=![]() ,
,
∴点P的坐标为(![]() ,2);
,2);
②点P在线段CA上时,4<t<6,Q只能在A点,
此时t=![]() ,
,
6﹣![]() ,
,
∴点P的坐标为(4,![]() );
);
综上所述,所求点P的坐标为(![]() ,2)或(
,2)或(![]() ,2)或(
,2)或(![]() ,2)或(4,
,2)或(4,![]() ).
).

 名校课堂系列答案
名校课堂系列答案【题目】某同学上学期的数学历次测验成绩如下表所示:
测验类别 | 平时测验 | 期中测验 | 期末测验 | ||
第1次 | 第2次 | 第3次 | |||
成绩 | 100 | 106 | 106 | 105 | 110 |
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数)。