ЬтФПФкШн
ЁОЬтФПЁПЭјёЋЕЭСфЛЏЮЪЬтвбОв§Ц№ЩчЛсИїНчЕФИпЖШЙизЂЃЌгаЙиВПУХдкШЋЙњЗЖЮЇФкЖд12Љ35ЫъЕФЭјёЋШЫШКНјааСЫМђЕЅЕФЫцЛњГщбљЕїВщЃЌЛцжЦГівдЯТСНЗљЭГМЦЭМЃЎ
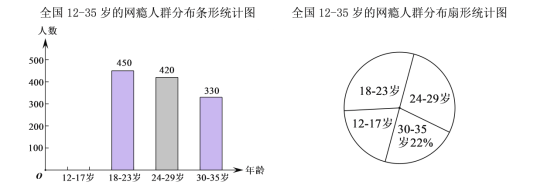
ЧыИљОнЭМжаЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮГщбљЕїВщжаЙВЕїВщСЫ ШЫЃЌВЂЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжа18Љ23ЫъВПЗжЕФдВаФНЧЕФЖШЪ§ЪЧ ЖШЃЛ
ЃЈ3ЃЉОнБЈЕРЃЌФПЧАЮвЙњ12Љ35ЫъЭјёЋШЫЪ§дМЮЊ3600ЭђЃЌЧыЙРМЦЦфжа12Љ23ЫъЕФШЫЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1500ЃЛЃЈ2ЃЉ108ЃЛЃЈ3ЃЉЙРМЦЦфжа12Љ23ЫъЕФШЫЪ§ЮЊ1800ЭђЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн30-35ЫъЕФШЫЪ§Г§вдЫљеМЕФАйЗжБШЃЌПЩЕУЕїВщЕФШЫЪ§ЃЛИљОнгаРэЪ§ЕФМѕЗЈЃЌПЩЕУ12-17ЫъЕФШЫЪ§ЃЛ
ЃЈ2ЃЉИљОн18-23ЫъЕФШЫЪ§Г§вдГщВщЕФШЫЪ§ГЫвд360ЁуЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнзмШЫЪ§ГЫвд12-23ЫъЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌПЩЕУД№АИЃЎ
ЃЈ1ЃЉетДЮГщбљЕїВщжаЙВЕїВщСЫ330ЁТ22%=1500ЃЈШЫЃЉЃЌ
12-17ЫъЕФШЫЪ§ЮЊЃК1500-450-420-330=300ЃЈШЫЃЉЃЌ
ВЙШЋЬѕаЮЭМШчЭМЃК
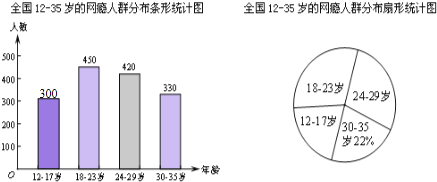
ЃЈ2ЃЉЩШаЮЭГМЦЭМжа18-23ЫъВПЗжЕФдВаФНЧЕФЖШЪ§ЪЧ![]() ЁС360Ёу=108ЁуЃЛ
ЁС360Ёу=108ЁуЃЛ
ЃЈ3ЃЉ3600ЁС![]() =1800ЃЈЭђШЫЃЉЃЌ
=1800ЃЈЭђШЫЃЉЃЌ
Д№ЃКЙРМЦЦфжа12-23ЫъЕФШЫЪ§дМ1800ЭђШЫЃЎ
ЙЪД№АИЮЊЃКЃЈ1ЃЉ1500ЃЛЃЈ2ЃЉ108ЃЎ

ЁОЬтФПЁПЮЊСЫНтФГаЃбЇЩњЕФЩэИпЧщПіЃЌЫцЛњГщШЁИУаЃФаЩњЁЂХЎЩњНјааЕїВщЃЌвбжЊГщШЁЕФбљБОжаЃЌФаЩњКЭХЎЩњЕФШЫЪ§ЯрЭЌЃЌРћгУЫљЕУЪ§ОнЛцжЦШчЯТЭГМЦЭМБэЃК
ЩэИпЧщПіЗжзщБэЃЈЕЅЮЛЃКcmЃЉ
зщБ№ | ЩэИп |
|
|
|
|
|
|
|
|
|
|
ФаЩњЩэИпЧщПіжБЗНЭМ
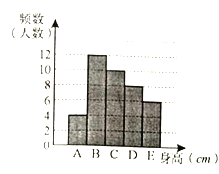
ХЎЩњЩэИпЧщПіЩШаЮЭГМЦЭМ
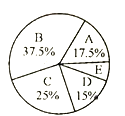
ИљОнЭМБэЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓбљБОжаФаЩњЕФШЫЪ§.
ЃЈ2ЃЉЧѓбљБОжаХЎЩњЩэИпдкEзщЕФШЫЪ§.
ЃЈ3ЃЉвбжЊИУаЃЙВгаФаЩњ380ШЫЃЌХЎЩњ320ШЫЃЌЧыЙРМЦШЋаЃЩэИпдк![]() жЎМфЕФбЇЩњзмШЫЪ§.
жЎМфЕФбЇЩњзмШЫЪ§.