Question

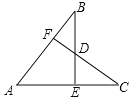
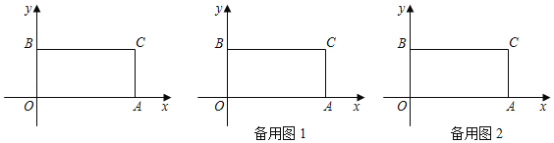
【题目】如图，在菱形ABCD中，∠BAD＝60°，AB＝2，E是DC边上一个动点，F是AB边上一点，∠AEF＝30°．设DE＝x，图中某条线段长为y，y与x满足的函数关系的图象大致如图所示，则这条线段可能是图中的（　　）．

A. 线段EC B. 线段AE C. 线段EF D. 线段BF

Answer 1

【答案】B

【解析】求出当点E与点D重合时，即x=0时EC、AE、EF、BF的长可排除C、D；当点E与点C重合时，即x=2时，求出EC、AE的长可排除A，可得答案．

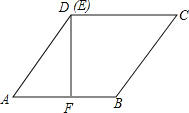
当点E与点D重合时，即x=0时，EC=DC=2，AE=AD=2，

∵∠A=60°，∠AEF=30°，

∴∠AFD=90°，

在Rt△ADF中，∵AD=2，

∴AF=AD=1，EF=DF=ADcos∠ADF=，

∴BF=AB-AF=1，结合图象可知C、D错误；

当点E与点C重合时，即x=2时，

如图，连接BD交AC于H，

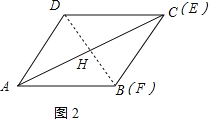
此时EC=0，故A错误；

∵四边形ABCD是菱形，∠BAD=60°，

∴∠DAC=30°，

∴AE=2AH=2ADcos∠DAC=2×2×=2，故B正确．

故选：B．