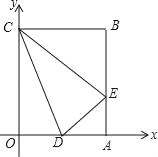
题目内容
【题目】如图,已知直线![]() 与坐标轴交于
与坐标轴交于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 轴正半轴上一点,并且
轴正半轴上一点,并且![]() ,点
,点![]() 是线段
是线段![]() 上一动点(不与端点重合),过点
上一动点(不与端点重合),过点![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() .
.
(1)求![]() 所在直线的解析式;
所在直线的解析式;
(2)若![]() 轴于
轴于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 与
与![]() 的长;
的长;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为等腰直角三角形?若存在,请直接写出点
为等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
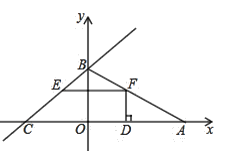
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在满足条件的点
;(3)存在满足条件的点![]() ,其坐标为
,其坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)由直线![]() 可求得
可求得![]() 、
、![]() 坐标,再结合
坐标,再结合![]() ,则可求得
,则可求得![]() 点坐标,利用待定系数法可求得直线
点坐标,利用待定系数法可求得直线![]() 的解析式;
的解析式;
(2)根据直线![]() 解析式可求得
解析式可求得![]() 点的纵坐标,即可表示出
点的纵坐标,即可表示出![]() 的长,由
的长,由![]() 轴则可得出
轴则可得出![]() 点纵坐标,代入直线
点纵坐标,代入直线![]() 解析式可求得
解析式可求得![]() 点横坐标,从而可表示出
点横坐标,从而可表示出![]() 的长;
的长;
(3)设![]() ,当
,当![]() 时,则有
时,则有![]() ,则可得到关于x的方程,可求得
,则可得到关于x的方程,可求得![]() 点坐标;当
点坐标;当![]() 时,则有
时,则有![]() ,可求得
,可求得![]() 点坐标;当
点坐标;当![]() 时,过
时,过![]() 作
作![]() ,由等腰直角三角形的性质可知
,由等腰直角三角形的性质可知![]() ,可求得
,可求得![]() 点坐标,从而可求得
点坐标,从而可求得![]() 点坐标.
点坐标.
解:
(1)在![]() 中,令
中,令![]() 可得
可得![]() ,令
,令![]() 可求得
可求得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
![]()
![]() ,解得
,解得 ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ;
;
(2)![]() 轴,且
轴,且![]() ,
,
![]() 点横坐标为
点横坐标为![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 点纵坐标为
点纵坐标为![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() 在线段
在线段![]() 上,
上,
![]()
![]() ;
;
(3)假设存在满足条件的点![]() ,设其坐标为
,设其坐标为![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 有
有![]() 、
、![]() 和
和![]() 三种情况,
三种情况,
①当![]() 时,则有
时,则有![]() ,
,
由(2)可得![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
②当![]() 时,则有
时,则有![]() ,
,
在![]() 中,令
中,令![]() 可得
可得![]() ,
,
![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
③当![]() 时,如图,过
时,如图,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
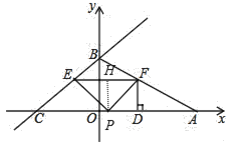
由(2)可知![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
综上可知存在满足条件的点![]() ,其坐标为
,其坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]()