题目内容
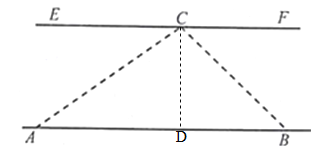
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
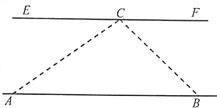
【答案】湛河的宽度约60米
【解析】试题分析:过C作CD⊥AB于点D,设CD=x米.由∠CBD=45°,得到BD=CD=x .
在Rt△ADC中,用tan∠CAD表示出AD .根据AB=AD+DB=140,列方程求解即可.
试题解析:解:过C作CD⊥AB于点D,设CD=x米.
在Rt△BDC中,∠CDB=90°,∠CBD=45°,∴BD=CD=x .
在Rt△ADC中,∠ADC=90°,∠CAD=37°,∴AD=![]() .
.
∵AB=AD+DB=140,∴![]() ,∴x=60.
,∴x=60.
答:湛河的宽度约60米.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目