题目内容
【题目】已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°得到△DEC。
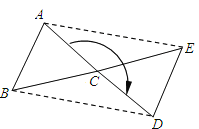
(1)试猜想AE与BD有何关系?说明理由;
(2)请给△ABC添加一个条件,使旋转得到的四边形ABDE为矩形,并说明理由
【答案】(1)AE∥BD,且AE=BD.理由见解析;(2)AC=BC.理由见解析.
【解析】
试题分析:(1)根据旋转的性质推知四边形ABDE是平行四边形,则平行四边形的对边平行且相等,即AE∥BD,且AE=BD;
(2)AC=BC.根据旋转是性质可以推知平行四边形ABDE的对角线AD=BE,则该平行四边形是矩形.
试题解析:(1)AE∥BD,且AE=BD.理由如下:
∵将△ABC绕点C顺时针旋转180°得到△DEC,
∴△ABC≌△DEC,
∴AB=DE,∠ABC=∠DEC,
∴AB∥DE,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD;
(2)AC=BC.理由如下:
∵AC=BC,
∴根据旋转的性质推知AC=BC=CE=CD,
∴AD=BE,
又由(1)知,四边形ABDE是平行四边形,
∴四边形ABDE为矩形.

练习册系列答案
相关题目